Question

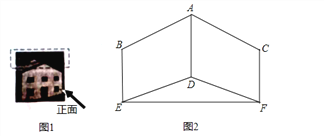
【题目】如图，图1是某仓库的实物图片，图2是该仓库屋顶（虚线部分）的正面示意图，BE、CF关于AD轴对称，且AD、BE、CF都与EF垂直，AD=3米，在B点测得A点的仰角为30°，在E点测得D点的仰角为20°，EF=6米，求BE的长．（结果精确到0.1米，参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，≈1.73）

Answer 1

【答案】BE的长约为2.4米.

【解析】延长AD交EF于点M，过B作BN⊥AD于点N，可证四边形BEMN为矩形，分别在Rt△ABN和Rt△DEM中求出AN、DM的长度，即可求得BE=MN=AD-AN+DM的长度．

解：延长AD交EF于点M，过B作BN⊥AD于点N，

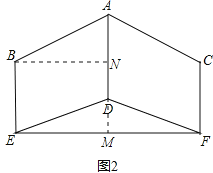
∵BE、CF关于AD轴对称，且AD、BE、CF都与EF垂直，
∴四边形BEMN为矩形，EM=MF=EF=3米，
∴BN=EM=3米，BE=MN，
在Rt△ABN中，
∵∠ABN=30°，BN=3米，=tan30°，
∴AN=BNtan30°=3×=（米），
在Rt△DEM中，
∵∠DEM=20°，EM=3米，=tan20°，
∴DM=EMtan20°≈3×0.36=1.08（米），
∴BE=MN=（AD-AN）+DM=3-+1.08≈3-1.73+1.08=2.35≈2.4（米）．
答：BE的长度为2.4米．

“点睛”本题考查了解直角三角形的应用，解答本题的关键是根据仰角和俯角的知识构造直角三角形，运用解直角三角形的知识分别求出AN、DM的长度，难度适中．