
【题目】如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m﹣3)2+n2﹣6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点. 
(1)求m、n的值并写出A、B、C三点的坐标;
(2)若OF+BE=AB,求证:CF=CE.
【答案】
(1)解:将(m﹣3)2+n2=6n﹣9变形得:(m﹣3)2+(n﹣3)2=0,
∴m=3,n=3,
∴A(3,3),B(3,0),C(0,3)
(2)解:∵OF+BE=AB,AE+EB=AB,
∴AE=OF,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COF=90°,
在△ACE和△OCF中,
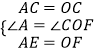 ,
,
∴△ACE≌△OCF(SAS),
∴CF=CE;
【解析】(1)已知等式变形后,利用非负数的性质求出m与n的值,即可确定出A,B,C的坐标;(2)由AE+EB=AB,以及OF+BE=AB,得到AE=OF,根据四边形ABOC为正方形,得到CA=CO,且∠A=∠COF=90°,利用SAS得到三角形ACE与三角形OCF全等,利用全等三角形对应边相等得到CF=CE;


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且![]() =PEPO.
=PEPO.
(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.

(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
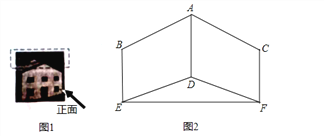
【题目】如图,图1是某仓库的实物图片,图2是该仓库屋顶(虚线部分)的正面示意图,BE、CF关于AD轴对称,且AD、BE、CF都与EF垂直,AD=3米,在B点测得A点的仰角为30°,在E点测得D点的仰角为20°,EF=6米,求BE的长.(结果精确到0.1米,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,中国高铁发展迅速,高铁技术不断走出国门,成为展示我国实力的新名片.预计到2015年底,中国高速铁路营运里程将达到18000公里.将18000用科学记数法表示应为( )
A.18×103
B.1.8×103
C.1.8×104
D.1.8×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿射线AB,BC运动,且它们的速度都为2cm/s.设点P的运动时间为t(s). 
(1)当t为何值时,△ABQ≌△CBP.
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列的调查中,选取的样本具有代表性的有 ( )
A.为了解某地区居民的防火意识,对该地区的初中生进行调查
B.为了解某校1200名学生的视力情况,随机抽取该校120名学生进行调查
C.为了解某商场的平均晶营业额,选在周末进行调查
D.为了解全校学生课外小组的活动情况,对该校的男生进行调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com