
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 为标准,超过和不足的千克数分别用正、负数来表述,记录如下:
为标准,超过和不足的千克数分别用正、负数来表述,记录如下:
与标准质量的差值 |
|
|
|
|
|
|
筐数 |
|
|
|
|
|
|
(1)![]() 筐白菜中,最重的一筐和最轻的一筐重_______________.
筐白菜中,最重的一筐和最轻的一筐重_______________.
(2)![]() 筐白菜实际总重量与标准总重量相比是超过还是不足?超过或不足多少千克?
筐白菜实际总重量与标准总重量相比是超过还是不足?超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
【答案】(1)5.5千克;(2)超过,8千克;(3)1320.8元
【解析】
(1)根据最大数减最小数,可得答案;
(2)根据有理数的加法,可得标准的重量,根据有理数的大小比较,可得答案;
(3)根据有理数的加法,可得总重量,根据单价乘以数量,可得答案.
解:(1)最重的一筐比最轻的一筐多重:2.5-(-3)=2.5+3=5.5(千克),
∴20筐白菜中,最重的一筐比最轻的一筐多重5.5千克;
故答案为:5.5千克;
(2)-3×1+(-2)×4+(-1.5)×2+0×3+1×2+2.5×8
=![]()
=![]() (千克);
(千克);
∴20筐白菜总计超过标准总重量8千克;
(3)由(2)可知,20筐白菜总计超过标准总重量8千克,
∴![]() (元);
(元);
∴白菜每千克售价2.6元,则出售这20筐白菜可卖1320.8元.


科目:初中数学 来源: 题型:
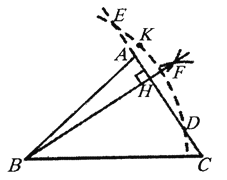
【题目】小明用尺规作图作△ABC的边AC上的高BH,作法如下:
① 分别以点D、E为圆心,大于DE的一半的长度为半径作弧,两弧交于点F;
② 作射线BF,交边AC于点H;
③ 以B为圆心,BK的长为半径作弧,交直线AC于点D和E;
④ 取一点K,使K和B在AC的两侧;
⑤ 所以BH就是所求作的高。
正确的作图顺序应该是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,第2018次输出的结果为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
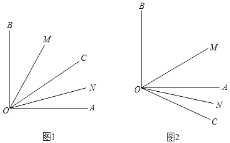
【题目】已知∠AOB=90°,OC是一条可以绕点O转动的射线,ON平分∠AOC,OM平分∠BOC.
(1)当射线OC转动到∠AOB的内部时,如图(1),求∠MON得度数.
(2)当射线OC转动到∠AOB的外时(90°<∠BOC<∠180°),如图2,∠MON的大小是否发生变化,变或者不变均说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
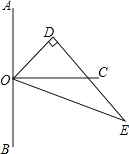
【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
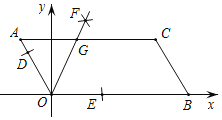
【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A. (![]() ﹣1,2) B. (
﹣1,2) B. (![]() ,2) C. (3﹣
,2) C. (3﹣![]() ,2) D. (
,2) D. (![]() ﹣2,2)
﹣2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点![]() 对应的数分别为-1,0,3,点
对应的数分别为-1,0,3,点![]() 为数轴上任意一点,其对应的数为
为数轴上任意一点,其对应的数为![]() .
.
(1)![]() 的长为_______;
的长为_______;
(2)如果点![]() 到点
到点![]() 、点
、点![]() 的距离相等,那么
的距离相等,那么![]() 的值是_______;
的值是_______;
(3)若点![]() 到点
到点![]() 、点
、点![]() 的距离之和是8,那么
的距离之和是8,那么![]() 的值是_______;
的值是_______;
(4)如果点![]() 以每分钟1个单位长度的速度从点
以每分钟1个单位长度的速度从点![]() 向左运动,同时点
向左运动,同时点![]() 和点
和点![]() 分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设
分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设![]() 分钟时点P到点
分钟时点P到点![]() 、点
、点![]() 的距离相等,那么
的距离相等,那么![]() 的值是_______.
的值是_______.
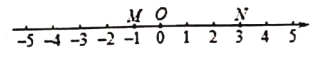
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com