
【题目】已知∠AOB=90°,OC是一条可以绕点O转动的射线,ON平分∠AOC,OM平分∠BOC.
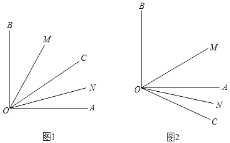
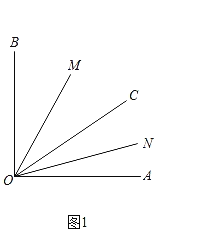
(1)当射线OC转动到∠AOB的内部时,如图(1),求∠MON得度数.
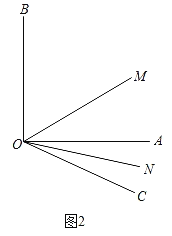
(2)当射线OC转动到∠AOB的外时(90°<∠BOC<∠180°),如图2,∠MON的大小是否发生变化,变或者不变均说明理由.
【答案】(1)45°;(2)∠MON的大小不变,理由见解析.
【解析】
(1)由角平分线的定义,求得∠CON=![]() ,∠COM=
,∠COM=![]() ,然后利用角的和差计算∠MON的度数为45°;
,然后利用角的和差计算∠MON的度数为45°;
(2)由角平分线的定义,求得∠CON=![]() ,∠COM=
,∠COM=![]() ,然后利用角的和差计算∠MON的度数为45°,从而求得结论.
,然后利用角的和差计算∠MON的度数为45°,从而求得结论.
解:(1)如图1所示:
∵ON平分∠AOC,
∴∠CON=![]() ,
,
又∵OM平分∠BOC,
∴∠COM=![]() ,
,
又∵∠AOB=∠AOC+∠BOC=90°,
∴∠MON=∠CON+∠OMC
=![]()
=![]()
=45°;
(2)∠MON的大小不变,如图2所示,理由如下:
∵OM平分∠BOC,
∴∠MOC=![]() ,
,
又∵ON平分∠AOC,
∴∠AON=![]() ,
,
又∵∠MON=∠AON+∠AOM,
∴∠MON=![]()
=![]()
=![]()
=45°.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
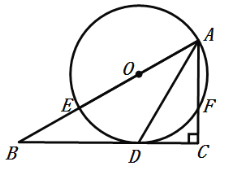
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
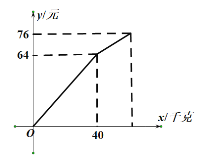
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
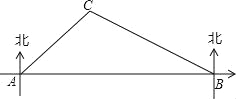
【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 为标准,超过和不足的千克数分别用正、负数来表述,记录如下:
为标准,超过和不足的千克数分别用正、负数来表述,记录如下:
与标准质量的差值 |
|
|
|
|
|
|
筐数 |
|
|
|
|
|
|
(1)![]() 筐白菜中,最重的一筐和最轻的一筐重_______________.
筐白菜中,最重的一筐和最轻的一筐重_______________.
(2)![]() 筐白菜实际总重量与标准总重量相比是超过还是不足?超过或不足多少千克?
筐白菜实际总重量与标准总重量相比是超过还是不足?超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
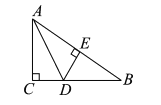
【题目】如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AC=3cm,BC=5cm,则三角形BDE的周长是_________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com