
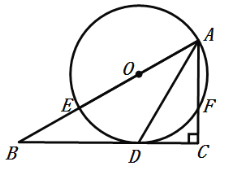
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
【答案】(1)证明见解析;(2)![]()
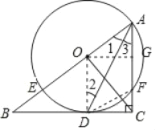
【解析】试题分析:(1)连接OD,由 OD=OA,可得∠1=∠2,再由BC为⊙O的切线,根据切线的性质可得∠ODB=90°,已知∠C=90°,所以∠ODB=∠C,即可判定OD∥AC,根据平行线的性质可得∠3=∠2,所以∠1=∠3,即可判定AD是∠BAC的平分线;(2)连接DF,已知∠B=30°,可求得∠BAC=60°,再由AD是∠BAC的平分线,可得∠3=30°,已知BC是⊙O的切线,根据弦切角定理可得∠FDC=∠3=30°,所以CD=![]() CF=
CF=![]() ,同理可得AC=
,同理可得AC=![]() CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=
CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=![]() AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=
AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=![]() ,由勾股定理可得OC=
,由勾股定理可得OC=![]() .
.
试题解析:
(1)证明:连接OD,∴OD=OA,∴∠1=∠2,
∵BC为⊙O的切线,∴∠ODB=90°,∵∠C=90°,∴∠ODB=∠C,∴OD∥AC,
∴∠3=∠2,∴∠1=∠3,∴AD是∠BAC的平分线;
(2)解:连接DF,∵∠B=30°,∴∠BAC=60°,
∵AD是∠BAC的平分线,∴∠3=30°,∵BC是⊙O的切线,∴∠FDC=∠3=30°,
∴CD=![]() CF=
CF=![]() ,∴AC=
,∴AC=![]() CD=3,∴AF=2,
CD=3,∴AF=2,
过O作OG⊥AF于G,∴GF=AF=1,四边形ODCG是矩形,
∴CG=2,OG=CD=![]() ,∴OC=
,∴OC=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
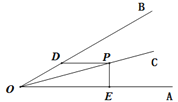
【题目】如图,∠AOB=30°,OC平分∠AOB,P为OC上任意一点,PD∥OA交OB于D,PE⊥OA于E,若OD=4,则PE= __________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,10个完全相同的棱长为2cm的小正方体堆成一个几何体.
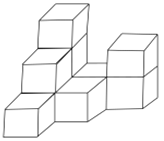
(1)画出从左面看和从上面看的形状图.
(2)如果在这个几何体的表面(不含底面)喷上黄色的漆,这个几何体喷漆的面积是多少cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
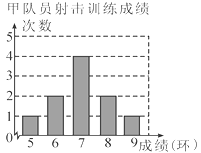
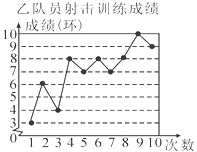
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
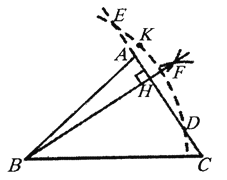
【题目】小明用尺规作图作△ABC的边AC上的高BH,作法如下:
① 分别以点D、E为圆心,大于DE的一半的长度为半径作弧,两弧交于点F;
② 作射线BF,交边AC于点H;
③ 以B为圆心,BK的长为半径作弧,交直线AC于点D和E;
④ 取一点K,使K和B在AC的两侧;
⑤ 所以BH就是所求作的高。
正确的作图顺序应该是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
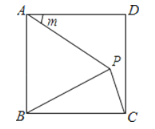
【题目】如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为________
查看答案和解析>>
科目:初中数学 来源: 题型:
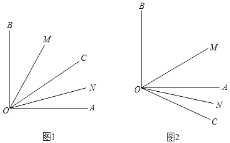
【题目】已知∠AOB=90°,OC是一条可以绕点O转动的射线,ON平分∠AOC,OM平分∠BOC.
(1)当射线OC转动到∠AOB的内部时,如图(1),求∠MON得度数.
(2)当射线OC转动到∠AOB的外时(90°<∠BOC<∠180°),如图2,∠MON的大小是否发生变化,变或者不变均说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com