
【题目】A、B两个港口相距100海里,港口B在港口A的北偏东31°方向上,有一艘船从A港口出发,沿北偏西44°方向匀速行驶3小时后,到达位于B港口南偏西76°方向的C处.求此船行驶的速度(结果精确到1海里/时,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
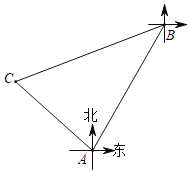
【答案】27海里/时
【解析】
利用方向角的定义得到∠1=∠2=31°,则∠BAC=31°+44°=75°,∠ABC=76°﹣31°=45°,在利用三角形内角和得到∠ACB=60°,作AH⊥BC于H,如图,在Rt△ABH中,利用等腰直角三角形的性质得BH=AH=50![]() 在Rt△ACH中,利用含30度的直角三角形三边的关系得到CH=
在Rt△ACH中,利用含30度的直角三角形三边的关系得到CH=![]() AH=
AH=![]() ,AC=2CH=
,AC=2CH=![]() ,然后计算此船行驶的速度.
,然后计算此船行驶的速度.
根据题意得∠1=∠2=31°,
∠BAC=31°+44°=75°,∠ABC=76°﹣31°=45°,
∴∠ACB=180°﹣75°﹣45°=60°,
作AH⊥BC于H,如图,
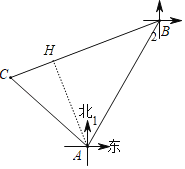
在Rt△ABH中,BH=AH=![]() AB=50
AB=50![]() ,
,
在Rt△ACH中,CH=![]() AH=
AH=![]() ×50
×50![]() =
=![]() ,
,
AC=2CH=![]() ,
,
∴此船行驶的速度=![]() =
=![]() ≈27.
≈27.
答:此船行驶的速度为27海里/时.


科目:初中数学 来源: 题型:
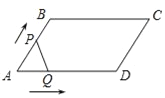
【题目】如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从 顶点A出发,点P沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x的函数图象大致是( )
A. 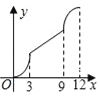 B.
B. 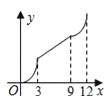 C.
C. 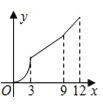 D.
D. 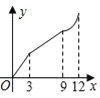
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
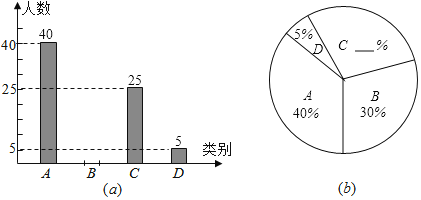
【题目】为了了解某区2018年初中毕业生毕业后的去向,某区教育部门对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中;C,直接进入社会就业;D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问:
(1)此次共调查了多少名初中毕业生?
(2)将两幅统计图中不完整的部分补充完整;
(3)若某区2018年初三毕业生共有3500人,请估计2019年初三毕业生中读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有22名工人,每人每天可生产1200个螺钉或2000个螺母,1个螺钉需配2个螺母,为使生产的螺钉和螺母刚好配套,若设x名工人生产螺钉,依题意列方程为( )
A. 1200x=2000(22-x) B. 1200x=2![]() 2000(22-x)
2000(22-x)
C. 1200(22-x)=2000x D. 2![]() 1200x=2000(22-x)
1200x=2000(22-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多8元,用1800元购买的科普书的数量与用l000元购买的文学书的数量相同.
(1)求去年购买的文学书和科普书的单价各是多少元;
(2)这所学校今年计划再购买这两种文学书和科普书共200本,且购买文学书和科普书的总费用不超过2088元.今年文学书的单价比去年提高了20%,科普书的单价与去年相同,且每购买1本科普书就免费赠送1本文学书,求这所学校今年至少要购买多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
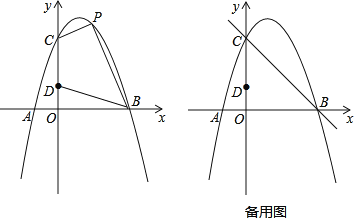
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题提出]
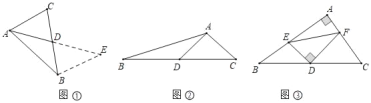
如图①,在△ABC中,若AB=6,AC=4,求BC边上的中线AD的取值范围.
[问题解决]
解决此问题可以用如下方法,延长AD到点E使DE=AD,再连结BE(或将△ACD绕着点D逆时针装转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断,由此得出中线AD的取值范围是
[应用]
如图②,如图,在△ABC中,D为边BC的中点,已知AB=5,AC=3,AD=2.求BC的长
[拓展]
如图③,在△ABC中,∠A=90°,点D是边BC的中点,点E在边AB上,过点D作DF⊥DE交边AC于点F,连结EF,已知BE=4,CF=5,则EF的长为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com