
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC. 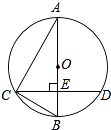
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的直径.
【答案】
(1)证明:连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,∠BCD与∠ACE互余;又∠ACE与∠CAE互余
∴∠BCD=∠BAC.
∵OA=OC,∴∠OAC=∠OCA.
∴∠ACO=∠BCD
(2)解:设⊙O的半径为Rcm,则OE=OB﹣EB=(R﹣8)cm,
CE= ![]() CD=
CD= ![]() ×24=12cm,
×24=12cm,
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R﹣8)2+122
解得R=13,∴2R=2×13=26cm.
答:⊙O的直径为26cm.
【解析】(1)根据垂径定理和圆的性质,同弧的圆周角相等,又因为△AOC是等腰三角形,即可求证.(2)根据勾股定理,求出各边之间的关系,即可确定半径.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=﹣ ![]() (x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=
(x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y= ![]() (k>0,x>0)于点P,且OAMP=12.
(k>0,x>0)于点P,且OAMP=12.
(1)求k的值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③ ![]() .其中正确的有( )
.其中正确的有( ) 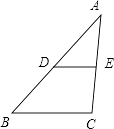
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.
(1)如图(1),当点E在BC边的中点位置时,通过测量AE,EM的长度,猜想AE与EM满足的数量关系是;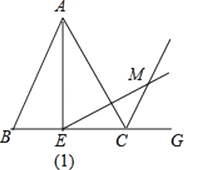
(2)如图(2),小晏通过观察、实验,提出猜想:当点E在BC边的任意位置时,始终有AE=EM.小晏把这个猜想与同学进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:在BA上取一点H使AH=CE,连接EH,要证AE=EM,只需证△AHE≌△ECM.
想法2:找点A关于直线BC的对称点F,连接AF,CF,EF.(易证∠BCF+∠BCA+ACM=180°,所以M,C,F三点在同一直线上)要证AE=EM,只需证△MEF为等腰三角形.
想法3:将线段BE绕点B顺时针旋转60°,得到线段BF,连接CF,EF,要证AE=EM,只需证四边形MCFE为平行四边形.
请你参考上面的想法,帮助小晏证明AE=EM.(一种方法即可)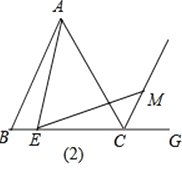
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点. 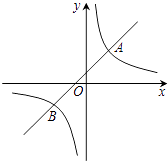
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1 , △2 , △3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( ) 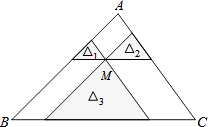
A.49
B.64
C.100
D.81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里) (参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.“射击运动员射击一次,命中靶心”是必然事件
B.不可能事件发生的概率为0
C.随机事件发生的概率为 ![]()
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,反比例函数y= ![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2 ![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D. 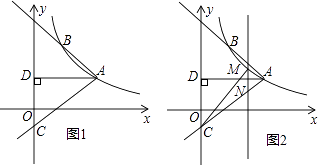
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2, 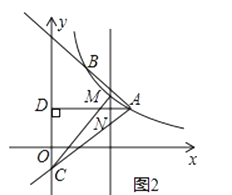
M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com