
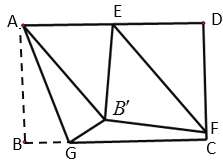
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的一个动点,点
的一个动点,点![]() 是线段
是线段![]() 上的点,
上的点,![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() 为直角三角形,则
为直角三角形,则![]() 为________.
为________.
【答案】![]() 或
或![]()
【解析】
分类讨论:B’为直角顶点和E点为直角顶点,过B’作AB的平行线角AD、BC于点M和N,得到△AB’M∽△B’NG由此求出B’N的长,再根据△B’ME∽△FH B’进而求出CF.
解:分类讨论:
第一种情况:当B’为直角顶角时,如下图所示:
过B’作AB的平行线角AD、BC于点M和N,过F点作FH⊥MN与H.
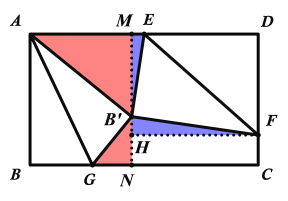
由折叠知:AB’=AB=6,BG’=BG=2,∠AB’G=∠B=90°
∴∠AB’M+∠GB’N=90°
又∠AB’M+∠B’AM=90°
∴∠GB’N=∠B’AM,且∠AMN=∠MNB=90°
∴△AB’M∽△B’NG,设B’N=x
则![]() ,代入数据:
,代入数据:![]() ,得
,得![]()
∴![]()
在Rt△GB’N中,由勾股定理有:![]() ,代入数据:
,代入数据:
![]() ,解得
,解得![]() (
(![]() 舍去)
舍去)
∴![]()
∵∠EB’M+∠FB’H=90°
又∠HFB’+∠FB’H=90°
∴∠EB’M=∠HFB’,且∠EMN=∠MNC=90°
∴△EB’M∽△B’HF
∴![]() ,代入数据:
,代入数据: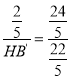 ,解得
,解得![]()
∴![]() .
.
第二种情况:当E为直角顶角时,如下图所示:
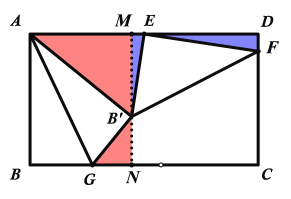
∵∠DEF+∠EFD=90°
又∠DEF+∠B’EM=90°
∴∠B’EM=∠EFD,且∠D=∠NME=90°
∴△DEF∽△EMB’
∴![]() ,由第一种情况知:
,由第一种情况知:![]() ,代入数据
,代入数据
∴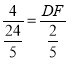 ,解得
,解得![]()
∴![]() .
.
故答案为:![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
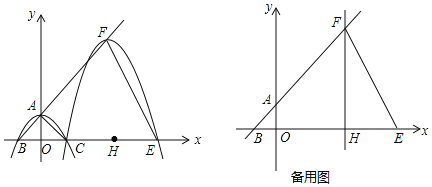
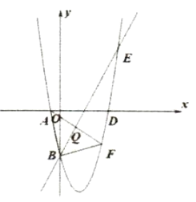
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B、C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
(1)求a、c的值;
(2)连接OF,求△OEF的周长;
(3)现将一足够大的三角板的直角顶点Q放在射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P,是否存在这样的点Q,使得以点P、Q、E为顶点的三角形与△POE全等?若存在,请直接写出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】面对疫情,每个人都需要积极行动起来,做好预防工作.为此某校开展了“新型冠状病毒肺炎”防控知识竞赛.现从该校五、六年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:A.
表示,共分成四组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
五年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
六年级10名学生的竞赛成绩在C组中的数据是:94,90,94
五、六年级抽取的学生竞赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
五年级 | 92 | 93 |
| 52 |
六年级 | 92 |
| 100 | 50.4 |
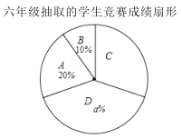
是据以上信息,解答下列问题:
(1)直接写出上述图表中![]() ,
,![]() ,
,![]() 的值:
的值:![]() __________,
__________,![]() ___________,
___________,![]() ___________;
___________;
(2)由以上数据,你认为该校五、六年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校五、六年级共1800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀![]() 的学生人数是多少?
的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则EF![]() ED的最小值为( )
ED的最小值为( )
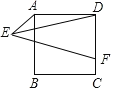
A.6![]() B.4C.4
B.4C.4![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.为了解全市中小学生对网络直播课的满意程度,应采用抽样调查
B.数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的方差为
的方差为![]()
C.三角形的的内心到三角形三边距离相等
D.顺次连接对角线垂直的四边形的中点,所形成的四边形为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,与直线
,与直线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,
轴上,![]() .
.
(1)求二次函数的解析式;
(2)在抛物线上有一点![]() ,若
,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)点![]() 在第四象限的抛物线上运动,连接
在第四象限的抛物线上运动,连接![]() ,与直线
,与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .设
.设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
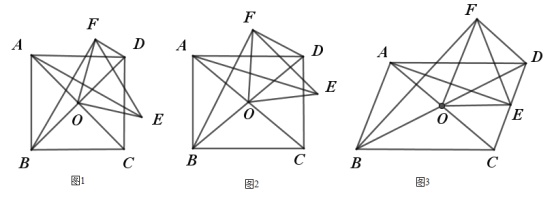
【题目】如图1,正方形ABCD的对角线AC,BD交于点O,将△COD绕点O逆时针旋转得到△EOF(旋转角为锐角),连AE,BF,DF,则AE=BF.
(1)如图2,若(1)中的正方形为矩形,其他条件不变.
①探究AE与BF的数量关系,并证明你的结论;
②若BD=7,AE=![]() ,求DF的长;
,求DF的长;
(2)如图3,若(1)中的正方形为平行四边形,其他条件不变,且BD=10,AC=6,AE=5,请直接写出DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020贺岁片《囧妈》提档大年三十网络首播.“乐调查”平台为了全面了解观众对《囧妈》的满意度情况,进行随机抽样调查,分为四个类别:![]() .非常满意;
.非常满意;![]() .满意;
.满意;![]() .基本满意;
.基本满意;![]() .不满意,依据调查数据绘制成图1和图2的统计图(不完整).
.不满意,依据调查数据绘制成图1和图2的统计图(不完整).
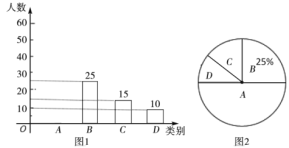
根据以上信息,解答下列问题:
(1)本次接受调查的观众共有_______人;
(2)扇形统计图中,扇形![]() 的圆心角度数是_______;
的圆心角度数是_______;
(3)请补全条形统计图;
(4)“乐调查”平台调查了春节期间观看《固妈》的观众约5000人,请估计观众对该电影的满意(![]() 、
、![]() 、
、![]() 类视为满意)的人数.
类视为满意)的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com