
【题目】如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则EF![]() ED的最小值为( )
ED的最小值为( )
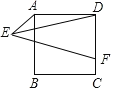
A.6![]() B.4C.4
B.4C.4![]() D.6
D.6
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,直线
,直线![]() 经过抛物线的顶点
经过抛物线的顶点![]() .已知该抛物线的对称轴为直线
.已知该抛物线的对称轴为直线![]() ,交
,交![]() 轴于点
轴于点![]() .
.
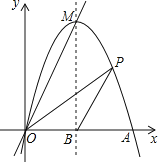
(1)求![]() 的值.
的值.
(2)![]() 是第一象限内抛物线上的一点,且在对称轴的右侧,连接
是第一象限内抛物线上的一点,且在对称轴的右侧,连接![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ;
;
①![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
②记![]() .求
.求![]() 关于
关于![]() 的函数表达式及
的函数表达式及![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 的顶点在
的顶点在![]() 上,
上,![]() 交直线
交直线![]() 于
于![]() 点.
点.
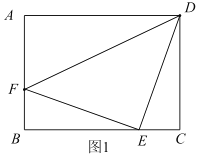

(1)如图1,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
(2)如图2,![]() ,当
,当![]() 时,求证:
时,求证:![]() 是
是![]() 的中点;
的中点;
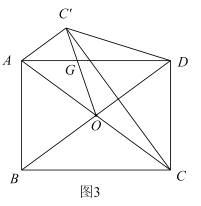
(3)如图3,若![]() ,对角线
,对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 的长,请直接写出答案.
的长,请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
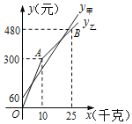
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与x之间的函数关系如图所示,折线OAB表示y乙与x之间的函数关系.
(1)甲采摘园的门票是 元,乙采摘园优惠前的草莓单价是每千克 元;
(2)当x>10时,求y乙与x的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
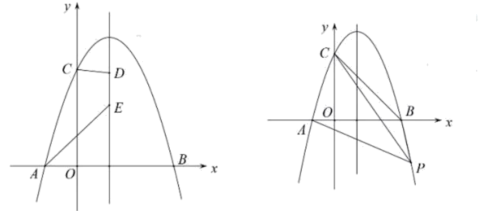
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
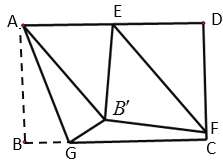
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的一个动点,点
的一个动点,点![]() 是线段
是线段![]() 上的点,
上的点,![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() 为直角三角形,则
为直角三角形,则![]() 为________.
为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生新冠疫情防控期间每天居家体育活动的时间(单位:![]() ),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
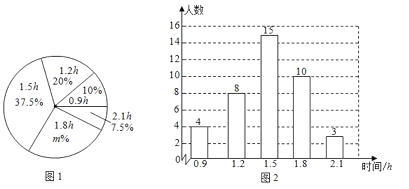
(1)本次接受调查的初中学生人数为________,图①中![]() 的值为________;
的值为________;
(2)这组数据的平均数是________,众数是________,中位数是________;
(3)根据统计的这组每天居家体育活动时间的样本数据,估计该校500名九年级学生居家期间每天体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,D为![]() 的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
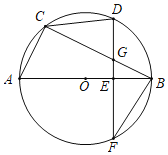
(1)求证:△BFG≌△DCG;
(2)若AC=10,BE=8,求BF的长;
(3)在(2)的条件下,P为⊙O上一点,连接BP,CP,弦CP交直径AB于点H,若△BPH与△CPB相似,求CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com