
【题目】四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 的顶点在
的顶点在![]() 上,
上,![]() 交直线
交直线![]() 于
于![]() 点.
点.
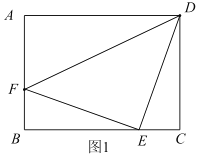

(1)如图1,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
(2)如图2,![]() ,当
,当![]() 时,求证:
时,求证:![]() 是
是![]() 的中点;
的中点;
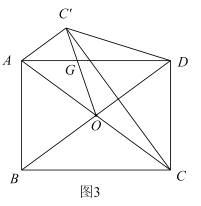
(3)如图3,若![]() ,对角线
,对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 的长,请直接写出答案.
的长,请直接写出答案.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)先证明![]() ,求出
,求出![]() ,
,![]() ,利用Rt
,利用Rt![]() 中,求出
中,求出![]() ,再利用等腰直角三角形的性质求出DF的长;
,再利用等腰直角三角形的性质求出DF的长;
(2)在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,得到
,得到![]() 为等边三角形,再证明得到
为等边三角形,再证明得到![]() ,根
,根![]() ,求出
,求出![]() ,故可得到
,故可得到![]() ,即可证明;
,即可证明;
(3)先利用![]() ,得到平行四边形
,得到平行四边形![]() 为矩形,设
为矩形,设![]() 与
与![]() 交点为
交点为![]() ,根据对称性得到OD垂直平分CC’,根据等积法求出CM,利用勾股定理求出OM,再根据中位线的性质求出AC’,利用平行线证明
,根据对称性得到OD垂直平分CC’,根据等积法求出CM,利用勾股定理求出OM,再根据中位线的性质求出AC’,利用平行线证明![]() ,得到
,得到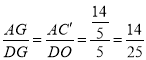 ,再根据AD=8,进而求出AG的长.
,再根据AD=8,进而求出AG的长.
(1)∵![]()
∴∠C=180°-∠B=90°,∠FEB+∠EFB=∠FEB+∠DEC=90°,
∴∠EFB=∠DEC
又![]()
∴![]() ,
,
∴![]()
∵![]()
∴![]() ,
,
在Rt![]() 中,
中,![]()
∵![]() ,
,![]()
∴△DEF是等腰直角三角形,
∴![]() ;
;
(2)证明:如图2,在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,则
,则![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]() ,
,![]() ,
,
∴![]() 是
是![]() 的中点.
的中点.
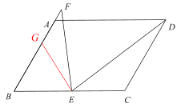
(3)解:由题意得,![]() 为线段
为线段![]() 的垂直平分线,设
的垂直平分线,设![]() 与
与![]() 交点为
交点为![]()
∵![]() ,
,
∴平行四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴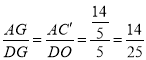 ,
,
∴![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数),当自变量
为常数),当自变量![]() 的值满足
的值满足![]() 时,与其对应的函数值
时,与其对应的函数值![]() 的最大值为-1,则
的最大值为-1,则![]() 的值为( )
的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,漏壶是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x(小时)表示漏水时间,y(厘米)表示壶底到水面的高度,某次计时过程中,记录到部分数据如下表:
漏水时间x(小时) | … | 3 | 4 | 5 | 6 | … |
壶底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种?求出该函数解析式及自变量x的取值范围;
(2)求刚开始计时时壶底到水面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明手中有4张背面相同的扑克牌:红桃6、红桃9、黑桃6、黑桃9.先将4张牌背面朝上洗匀,再让小丽抽牌.
(1)小丽从中任意抽取一张扑克牌,抽到黑桃9的概率是__________,抽到偶数的概率是_________;
(2)小丽从中任意抽取两张扑克牌,游戏规则规定:若小丽抽到的两张牌是一红一黑,则小丽胜,若小丽抽到的两张牌是一奇一偶,则小明胜,问该游戏对双方是否公平.(利用树状图或列表说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】面对疫情,每个人都需要积极行动起来,做好预防工作.为此某校开展了“新型冠状病毒肺炎”防控知识竞赛.现从该校五、六年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:A.
表示,共分成四组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
五年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
六年级10名学生的竞赛成绩在C组中的数据是:94,90,94
五、六年级抽取的学生竞赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
五年级 | 92 | 93 |
| 52 |
六年级 | 92 |
| 100 | 50.4 |
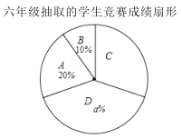
是据以上信息,解答下列问题:
(1)直接写出上述图表中![]() ,
,![]() ,
,![]() 的值:
的值:![]() __________,
__________,![]() ___________,
___________,![]() ___________;
___________;
(2)由以上数据,你认为该校五、六年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校五、六年级共1800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀![]() 的学生人数是多少?
的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
①cos(α+β)=cosαcosβ﹣sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;
②tan(α+β)=![]() .
.
③利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如tan105°=tan(45°+60°)=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
(1)求cos75°的值;
(2)如图,直升机在一建筑物CD上方的点A处测得建筑物顶端点D的俯角α为60°,底端点C的俯角β为75°,此时直升机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
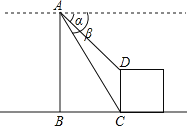
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则EF![]() ED的最小值为( )
ED的最小值为( )
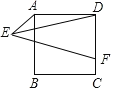
A.6![]() B.4C.4
B.4C.4![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,与直线
,与直线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,
轴上,![]() .
.
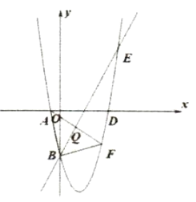
(1)求二次函数的解析式;
(2)在抛物线上有一点![]() ,若
,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)点![]() 在第四象限的抛物线上运动,连接
在第四象限的抛物线上运动,连接![]() ,与直线
,与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .设
.设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(m,0),m<0,点B与点A 关于原点对称,直线![]() 与双曲线
与双曲线![]() 交于C,D两点.
交于C,D两点.
(1)直接判断后填空:四边形ACBD的形状一定是 ;
(2)若点D(1,t),求双曲线的解析式;
(3)在(2)的前提下,四边形ACBD为矩形时,求m的值.
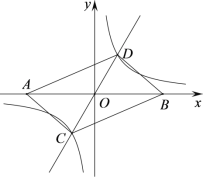
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com