
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),
∴根据题意,得![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)
解:由y=﹣x2+2x+3得,D点坐标为(1,4),
∴CD=![]() =
=![]() ,
,
BC=![]() =3
=3![]() ,
,
BD=![]() =2
=2![]() ,
,
∵CD2+BC2=(![]() )2+(3
)2+(3![]() )2=20,BD2=(2
)2=20,BD2=(2![]() )2=20,
)2=20,
∴CD2+BC2=BD2,
∴△BCD是直角三角形;
(3)
解:存在.
y=﹣x2+2x+3对称轴为直线x=1.
①若以CD为底边,则P1D=P1C,
设P1点坐标为(x,y),根据勾股定理可得P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,
因此2+(3﹣y)2=(x﹣1)2+(4﹣y)2,
即y=4﹣x.
又P1点(x,y)在抛物线上,
∴4﹣x=﹣x2+2x+3,
即x2﹣3x+1=0,
解得x1=![]() ,x2=
,x2=![]() <1,应舍去,
<1,应舍去,
∴x=![]() ,
,
∴y=4﹣x=![]() ,
,
即点P1坐标为(![]() ,
,![]() ).
).
②若以CD为一腰,
∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,
此时点P2坐标为(2,3).
∴符合条件的点P坐标为(![]() ,
,![]() )或(2,3).
)或(2,3).

【解析】(1)将A(﹣1,0)、B(3,0)代入二次函数y=ax2+bx﹣3a求得a、b的值即可确定二次函数的解析式;
(2)分别求得线段BC、CD、BD的长,利用勾股定理的逆定理进行判定即可;
(3)分以CD为底和以CD为腰两种情况讨论.运用两点间距离公式建立起P点横坐标和纵坐标之间的关系,再结合抛物线解析式即可求解.


科目:初中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F(1,0),且经过点
的右焦点为F(1,0),且经过点 ![]()
(1)求椭圆P的方程;
(2)已知正方形ABCD的顶点A,C在椭圆P上,顶点B,D在直线7x﹣7y+1=0上,求该正方形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB≠BC,连接AC,AE是∠BAD的平分线,交边DC的延长线于点F. 
(1)证明:CE=CF;
(2)若∠B=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.(如图2所示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为![]() 上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
(1)求证:QN=QF;
(2)若点E到弦MH的距离为1,cos∠Q=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生.
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若![]() =
=![]() ,则3S△BDG=13S△DGF .
,则3S△BDG=13S△DGF .
其中正确的结论是 写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1 , S2 . 若S=3,则S1+S2的值为( )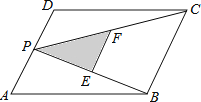
A.24
B.12
C.6
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从﹣2,﹣1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助九年级学生做好体育考试项目的选考工作,某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩,并绘制成如图两个统计图,请结合统计图信息解决问题.
(1)“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍,求“跳绳”项目的女生人数;
(2)若一个考试项目的男、女生总平均成绩不小于9分为“优秀”,试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目,并说明理由;
(3)请结合统计图信息和实际情况,给该校九年级学生体育考试项目的选择提出合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com