
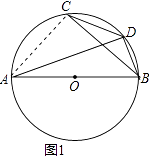
【题目】如图1,已知AB为⊙O的直径,点C为 ![]() 的中点,点D在
的中点,点D在 ![]() 上,连接BD、CD、BC、AD、BC与AD相交于点E.
上,连接BD、CD、BC、AD、BC与AD相交于点E. 
(1)求证:∠C+∠CBD=∠CBA;
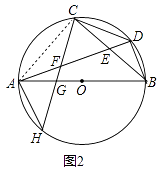
(2)如图2,过点C作CD的垂线,分别与AD,AB,⊙O相交于点F、G、H,求证:AF=BD; 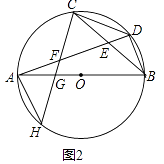
(3)如图3,在(2)的条件下,连接BF,若BF=BC,△CEF的面积等于3,求FG的长. 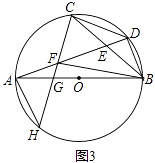
【答案】
(1)证明:连接AC,
在⊙O中,∵C为 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠CBA=∠CAB=∠CAD+∠DAB,
∵ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴∠DCB=∠DAB,∠CBD=∠CAD,
∴∠DCB+∠CBD=∠CAD+∠DAB=∠CAB=∠CBA
(2)证明:连接AC.
∵AB是直径,
∴∠ACB=90°=∠ACF+∠FCB,
∵CD⊥CH,
∴∠DCH=90°=∠FCB+∠DCB,
∴∠ACF=∠DCB,
∵ ![]() =
= ![]() ,
,
∴AC=BC,
在△ACF和△BCD中,
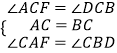 ,
,
∴△ACF≌△BCD,
∴AF=BD
(3)解:作BM⊥CH于M,AK⊥CH于K.
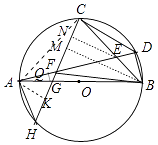
∴∠ACK+∠CAK=90°,∠AKC=∠BMC=90°,
∵∠ACB=90°,
∴∠ACK+∠KCB=90°,
∴∠CAK=∠KCB,∵AC=BC,
∴△ACK≌△CNM,
∴AK=CM,
∵CB=BF,BM⊥CF,
∴CM=FM=AK,
∵△ACF≌△BCD,
∴CF=CD,
∵∠FCD=90°,
∴∠CFD=∠CDF=45°=∠AFK,
∴△AFK是等腰直角三角形,
∴AK=FK=FM=CM,
在Rt△AKC中,tan∠CAK= ![]() =3,作EN⊥CH于N,
=3,作EN⊥CH于N,
在Rt△NCE中,∵∠HCB=∠CAK,
∴tan∠NCE= ![]() =3,设CN=m,EN=3m=NF,
=3,设CN=m,EN=3m=NF,
∴S△CEF= ![]() CFEN=
CFEN= ![]() ×(m+3m)×3m=3,
×(m+3m)×3m=3,
∴m= ![]() ,
,
∴CF=4m=2 ![]() ,
,
∴CM=FM=FK=AK= ![]() ,
,
∴AF=2,
∵ ![]() =
= ![]() ,
,
∴∠DCB=∠DAB=∠ACK,
过G作GQ⊥AF于Q,
在Rt△AQG中,tan∠FAB= ![]() =
= ![]() ,设QG=x,AQ=3x,FQ=x,
,设QG=x,AQ=3x,FQ=x,
∴4x=2,
∴x= ![]() ,
,
∴FG= ![]() x=
x= ![]()
【解析】(1)连接AC.由 ![]() =
= ![]() ,推出∠CBA=∠CAB=∠CAD+∠DAB,由
,推出∠CBA=∠CAB=∠CAD+∠DAB,由 ![]() =
= ![]() ,
, ![]() =
= ![]() ,推出∠DCB=∠DAB,∠CBD=∠CAD,推出∠DCB+∠CBD=∠CAD+∠DAB=∠CAB=∠CBA.(2)只要证明△ACF△BCD,即可推出AF=BD.(3)由△ACK≌△CNM,推出AK=CM,由△ACF≌△BCD,推出CF=CD,△AFK是等腰直角三角形,推出AK=FK=FM=CM,在Rt△AKC中,tan∠CAK=
,推出∠DCB=∠DAB,∠CBD=∠CAD,推出∠DCB+∠CBD=∠CAD+∠DAB=∠CAB=∠CBA.(2)只要证明△ACF△BCD,即可推出AF=BD.(3)由△ACK≌△CNM,推出AK=CM,由△ACF≌△BCD,推出CF=CD,△AFK是等腰直角三角形,推出AK=FK=FM=CM,在Rt△AKC中,tan∠CAK= ![]() =3,作EN⊥CH于N,在Rt△NCE中,由∠HCB=∠CAK,推出tan∠NCE=
=3,作EN⊥CH于N,在Rt△NCE中,由∠HCB=∠CAK,推出tan∠NCE= ![]() =3,设CN=m,EN=3m=NF,由S△CEF=
=3,设CN=m,EN=3m=NF,由S△CEF= ![]() CFEN=
CFEN= ![]() ×(m+3m)×3m,推出m=
×(m+3m)×3m,推出m= ![]() ,推出CF=4m=2
,推出CF=4m=2 ![]() ,推出CM=FM=FK=AK=
,推出CM=FM=FK=AK= ![]() ,AF=2,由
,AF=2,由 ![]() =
= ![]() ,推出∠DCB=∠DAB=∠ACK,过G作GQ⊥AF于Q,在Rt△AQG中,tan∠FAB=
,推出∠DCB=∠DAB=∠ACK,过G作GQ⊥AF于Q,在Rt△AQG中,tan∠FAB= ![]() =
= ![]() ,设QG=x,AQ=3x,FQ=x,可得4x=2,得x=
,设QG=x,AQ=3x,FQ=x,可得4x=2,得x= ![]() ,再根据FG=
,再根据FG= ![]() QG即可解决问题.
QG即可解决问题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)如果∠A=60°,则DE与DF有何数量关系?请说明理由;
(3)如果AB=5,BC=6,求tan∠BAC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前的单价x(元) | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后的单价y(元) | y1 | y2=4 | y3=59 | y4 | … | yn |
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为 ![]() ,
, ![]() ,猜想
,猜想 ![]() 与
与 ![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答). 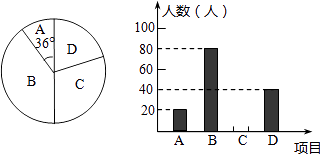
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则 ![]() 的值为
的值为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示. 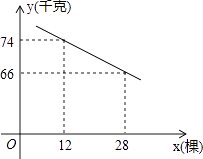
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.AC=18,BC=12,则△CEG的周长为 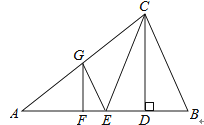
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com