Question

【题目】在平面直角坐标系中，点的坐标满足：

（1）求出点的坐标

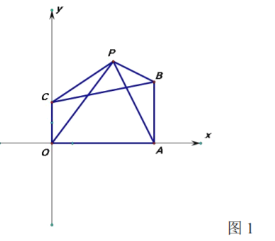
（2）如图1，连接，点在四边形外面且在第一象限，再连，则，求点坐标．

（3）如图2所示，为线段上一动点，（在右侧）为上一动点，使轴始终平分，连且，那么是否为定值？若为定值，请直接写出定值，若不是，请简单说明理由．

Answer 1

【答案】（1）A(5,0)，C(0,2)；（2）P(3, )；（3）是定值，∠F=2-180°.

【解析】

（1）根据绝对值和平方具有非负性得到2a-5c=0，c-2=0，解之即可得到a，c的值，从而得到A，C坐标；

（2）过P作PM⊥y轴，PN⊥AB的延长线，PH⊥x轴，因为，所以可得2PM=3PN，由图知PM+PN=5，可得PM=3，PN=2，由得，即，可求出PH的值，从而得到P点坐标；

（3）设∠CDF=，OE与DF的交点为M，由四边形内角和为360°，可得∠OMD的度数，根据三角形内角和为180°可得∠DEO的度数，根据已知可得∠DEF，而∠F=180°-∠DEF-∠FDE，将值代入即可求出∠F的度数.

解：（1）∵

∴

解得

∴A(5,0)，C(0,2)

（2）过P作PM⊥y轴，PN⊥AB的延长线，PH⊥x轴

由（1）知A(5,0)，C(0,2)，B(5,3)

∵

∴COPM=ABPN

∴×2PM=×3PN

∴2PM=3PN

∵PM+PN=5

∴PM=3，PN=2

∵

∴

∴

∴

即

∴PH=

∴P(3, )

（3）是定值，∠F=2-180°.

设∠CDF=

∴∠FDE=180°-2

设OE与DF的交点为M

∴∠OMD=360°---90°=270°--

∴∠DEO=∠OMD-∠FDE=90°+-

∴∠DEF=2∠DEO=180°+2-2

∴∠F=180°-∠DEF-∠FDE=2-180°

故答案为（1）A(5,0)，C(0,2)；（2）P(3, )；（3）是定值，∠F=2-180°.