
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯAЕуБэЪОЪ§aЃЌBЕуЪОЪ§bЃЌCЕуБэЪОЪ§cЃЌbЪЧзюаЁЕФе§ећЪ§ЃЌЧвaЁЂbТњзу|a+2|+ЃЈcЉ7ЃЉ2=0ЃЎ

ЃЈ1ЃЉa=ЁЁЁЁЃЌb=ЁЁЁЁЃЌc=ЁЁЁЁЃЛ
ЃЈ2ЃЉШєНЋЪ§жселЕўЃЌЪЙЕУAЕугыCЕужиКЯЃЌдђЕуBгыЪ§ЁЁЁЁБэЪОЕФЕужиКЯЃЛ
ЃЈ3ЃЉЕуAЁЂBЁЂCПЊЪМдкЪ§жсЩЯдЫЖЏЃЌШєЕуAвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЃЌЕуBКЭЕуCЗжБ№вдУПУы2ИіЕЅЮЛГЄЖШКЭ4ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌМйЩшtУыжгЙ§КѓЃЌШєЕуAгыЕуBжЎМфЕФОрРыБэЪОЮЊABЃЌЕуAгыЕуCжЎМфЕФОрРыБэЪОЮЊACЃЌЕуBгыЕуCжЎМфЕФОрРыБэЪОЮЊBCЃЎдђAB=ЁЁЁЁЃЌAC=ЁЁЁЁЃЌBC=ЁЁЁЁЃЎЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ4ЃЉЧыЮЪЃК3BCЉ2ABЕФжЕЪЧЗёЫцзХЪБМфtЕФБфЛЏЖјИФБфЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыЧѓЦфжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ-2ЃЌ 1ЃЌc=7ЃЛЃЈ2ЃЉ4ЃЛЃЈ3ЃЉ3t+3ЃЌ 5t+9ЃЌ 2t+6ЃЛЃЈ4ЃЉВЛБфЃЌ3BCЉ2AB=12ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУ|aЃЋ2|ЃЋЃЈc7ЃЉ2ЃН0ЃЌЕУaЃЋ2ЃН0ЃЌc7ЃН0ЃЌНтЕУaЃЌcЕФжЕЃЌгЩbЪЧзюаЁЕФе§ећЪ§ЃЌПЩЕУbЃН1ЃЛ
ЃЈ2ЃЉЯШЧѓГіЖдГЦЕуЃЌМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉABдРДЕФГЄЮЊ3ЃЌЫљвдABЃНtЃЋ2tЃЋ3ЃН3tЃЋ3ЃЌдйгЩACЃН9ЃЌЕУACЃНtЃЋ4tЃЋ9ЃН5tЃЋ9ЃЌгЩдРДBCЃН6ЃЌПЩжЊBCЃН4t2tЃЋ6ЃН2tЃЋ6ЃЛ
ЃЈ4ЃЉгЩ 3BC2ABЃН3ЃЈ2tЃЋ6ЃЉ2ЃЈ3tЃЋ3ЃЉЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЁп|aЃЋ2|ЃЋЃЈc7ЃЉ2ЃН0ЃЌ
ЁрaЃЋ2ЃН0ЃЌc7ЃН0ЃЌ
НтЕУaЃН2ЃЌcЃН7ЃЌ
ЁпbЪЧзюаЁЕФе§ећЪ§ЃЌ
ЁрbЃН1ЃЛ
ЙЪД№АИЮЊЃК2ЃЛ1ЃЛ7ЃЎ
ЃЈ2ЃЉЃЈ7ЃЋ2ЃЉЁТ2ЃН4.5ЃЌ
ЖдГЦЕуЮЊ74.5ЃН2.5ЃЌ
2.5ЃЋЃЈ2.51ЃЉЃН4ЃЛ
ЙЪД№АИЮЊЃК4ЃЎ
ЃЈ3ЃЉвРЬтвтПЩЕУABЃНtЃЋ2tЃЋ3ЃН3tЃЋ3ЃЌACЃНtЃЋ4tЃЋ9ЃН5tЃЋ9ЃЌBCЃН2tЃЋ6ЃЛ
ЙЪД№АИЮЊЃК3tЃЋ3ЃЛ5tЃЋ9ЃЛ2tЃЋ6ЃЎ
ЃЈ4ЃЉВЛБфЃЎ
3BC2ABЃН3ЃЈ2tЃЋ6ЃЉ2ЃЈ3tЃЋ3ЃЉЃН12ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
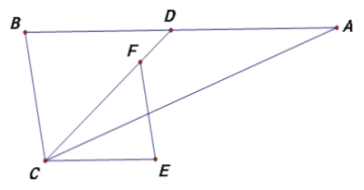
ЁОЬтФПЁПвбжЊЁїABCЮЊБпГЄЮЊ6ЕФЕШБпШ§НЧаЮЃЌDЃЌEЗжБ№дкБпBCЃЌACЩЯЃЌЧвCD=CE=xЃЌСЌНгDEВЂбгГЄжСЕуFЃЌЪЙEF=AEЃЌСЌНгAFЃЌCFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAEFЮЊЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮABDFЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉМЧЁїCEFЕФУцЛ§ЮЊSЃЌ
ЂйЧѓSгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЕБSгазюДѓжЕЪБЃЌХаЖЯCFгыBCЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪ§ТызЈгЊЕъЯњЪлМзЁЂввСНжжЦЗХЦжЧФмЪжЛњЃЌетСНжжЪжЛњЕФНјМлКЭЪлМлШчЯТБэЫљЪОЃК
Мз | вв | |
НјМлЃЈдЊ/ВПЃЉ | 4300 | 3600 |
ЪлМлЃЈдЊ/ВПЃЉ | 4800 | 4200 |
ЃЈ1ЃЉИУЕъЯњЪлМЧТМЯдЪОЃЎШ§дТЗнЯњЪлМзЁЂввСНжжЪжЛњЙВ17ВПЃЌЧвЯњЪлМзжжЪжЛњЕФРћШѓЧЁКУЪЧЯњЪлввжжЪжЛњРћШѓЕФ2БЖЃЌЧѓИУЕъШ§дТЗнЪлГіМзжжЪжЛњКЭввжжЪжЛњИїЖрЩйВПЃП
ЃЈ2ЃЉИљОнЪаГЁЕїбаЃЌИУЕъЫФдТЗнМЦЛЎЙКНјетСНжжЪжЛњЙВ20ВПЃЌвЊЧѓЙКНјввжжЪжЛњЪ§ВЛГЌЙ§МзжжЪжЛњЪ§ЕФ![]() ЃЌЖјгУгкЙКТђетСНжжЪжЛњЕФзЪН№ЕЭгк81500дЊЃЌЧыЭЈЙ§МЦЫуЩшМЦЫљгаПЩФмЕФНјЛѕЗНАИЃЎ
ЃЌЖјгУгкЙКТђетСНжжЪжЛњЕФзЪН№ЕЭгк81500дЊЃЌЧыЭЈЙ§МЦЫуЩшМЦЫљгаПЩФмЕФНјЛѕЗНАИЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌИУЕъДђЫуНЋЫФдТЗнАДМЦЛЎЙКНјЕФ20ВПЪжЛњШЋВПЪлГіКѓЃЌЫљЛёЕУРћШѓЕФ30%гУгкЙКТђAЃЌBСНПюНЬбЇвЧЦїОшдљИјФГЯЃЭћаЁбЇЃЎвбжЊЙКТђAвЧЦїУПЬЈ300дЊЃЌЙКТђBвЧЦїУПЬЈ570дЊЃЌЧвЫљОшЕФЧЎЧЁКУгУЭъЃЌЪдЮЪИУЕъОшдљAЃЌBСНПювЧЦївЛЙВЖрЩйЬЈЃПЃЈжБНгаДГіЫљгаПЩФмЕФНсЙћМДПЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкШ§НЧаЮ![]() жа,
жа, ![]() ,Еу
,Еу![]() ЪЧ
ЪЧ![]() ЩЯвЛЕу,Еу
ЩЯвЛЕу,Еу![]() ЪЧШ§НЧаЮЭтЩЯвЛЕу, Чв
ЪЧШ§НЧаЮЭтЩЯвЛЕу, Чв![]() Еу
Еу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§
ЕФЖШЪ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЕФзјБъТњзуЃК
ЕФзјБъТњзуЃК![]()
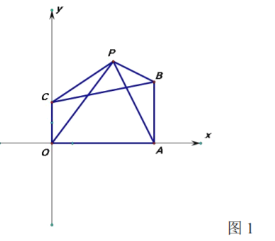
ЃЈ1ЃЉЧѓГіЕу![]() ЕФзјБъ
ЕФзјБъ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() дкЫФБпаЮ
дкЫФБпаЮ![]() ЭтУцЧвдкЕквЛЯѓЯоЃЌдйСЌ
ЭтУцЧвдкЕквЛЯѓЯоЃЌдйСЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕузјБъЃЎ
ЕузјБъЃЎ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЖЏЕуЃЌ
ЩЯвЛЖЏЕуЃЌ![]() ЃЈдк
ЃЈдк![]() гвВрЃЉЮЊ
гвВрЃЉЮЊ![]() ЩЯвЛЖЏЕуЃЌЪЙ
ЩЯвЛЖЏЕуЃЌЪЙ![]() жсЪМжеЦНЗж
жсЪМжеЦНЗж![]() ЃЌСЌ
ЃЌСЌ![]() Чв
Чв![]() ЃЌФЧУД
ЃЌФЧУД![]() ЪЧЗёЮЊЖЈжЕЃПШєЮЊЖЈжЕЃЌЧыжБНгаДГіЖЈжЕЃЌШєВЛЪЧЃЌЧыМђЕЅЫЕУїРэгЩЃЎ
ЪЧЗёЮЊЖЈжЕЃПШєЮЊЖЈжЕЃЌЧыжБНгаДГіЖЈжЕЃЌШєВЛЪЧЃЌЧыМђЕЅЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХњЗЂЩЬМЦЛЎНЋвЛХњКЃВњЦЗгЩAЕидЫЭљBЕиЃЎЦћГЕЛѕдЫЙЋЫОКЭЬњТЗЛѕдЫЙЋЫООљПЊАьКЃВњЦЗдЫЪфвЕЮёЃЎвбжЊдЫЪфТЗГЬЮЊ120ЧЇУзЃЌЦћГЕКЭЛ№ГЕЕФЫйЖШЗжБ№ЮЊ60ЧЇУзЃЏЪБЁЂ100ЧЇУзЃЏЪБЃЎСНЛѕдЫЙЋЫОЕФЪеЗбЯюФПМАЪеЗбБъзМШчЯТБэЫљЪОЃК
дЫЪфЙЄОп | дЫЪфЗбЕЅМлЃЏ (дЊЃЏЖжЁЄЧЇУз) | РфВиЗбЕЅМлЃЏ (дЊЃЏЖжЁЄаЁЪБ) | Й§ТЗЗбЃЏдЊ | зАаЖМАЙмРэЗбЃЏдЊ |
Цћ ГЕ | 2 | 5 | 200 | 0 |
Л№ ГЕ | 1.8 | 5 | 0 | 1600 |
зЂЃКЁАдЊЃЏЖжЁЄЧЇУзЁББэЪОУПЖжЛѕЮяУПЧЇУзЕФдЫЗбЃЛЁАдЊЃЏЖжЁЄаЁЪБЁББэЪОУПЖжЛѕЮяУПаЁЪБЕФРфВиЗбЃЎ
(1)ЩшИУХњЗЂЩЬД§дЫЕФКЃВњЦЗгаx(Жж)ЃЌЦћГЕЛѕдЫЙЋЫОКЭЬњТЗЛѕдЫЙЋЫОЫљвЊЪеШЁЕФЗбгУЗжБ№ЮЊy1(дЊ)КЭy2(дЊ)ЃЌЪдЧѓy1ЁЂy2гыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
(2)ШєИУХњЗЂЩЬД§дЫЕФКЃВњЦЗВЛЩйгк30ЖжЃЌЮЊНкЪЁдЫЗбЃЌЫћгІбЁдёФФИіЛѕдЫЙЋЫОГаЕЃдЫЪфвЕЮё?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЭЌбЇдкбЇЯАСЫШЋЕШШ§НЧаЮЕФЯрЙижЊЪЖКѓЗЂЯжЃЌжЛгУСНАбЭъШЋЯрЭЌЕФГЄЗНаЮжБГпОЭПЩвдзїГівЛИіНЧЕФЦНЗжЯпЃЎШчЭМЃКвЛАбжБГпбЙзЁЩфЯпOBЃЌСэвЛАбжБГпбЙзЁЩфЯпOAВЂЧвгыЕквЛАбжБГпНЛгкЕуPЃЌаЁУїЫЕЃКЁАЩфЯпOPОЭЪЧЁЯBOAЕФНЧЦНЗжЯпЃЎЁБЫћетбљзіЕФвРОнЪЧ(ЁЁЁЁ)

A. НЧЕФФкВПЕННЧЕФСНБпЕФОрРыЯрЕШЕФЕудкНЧЕФЦНЗжЯпЩЯ
B. НЧЦНЗжЯпЩЯЕФЕуЕНетИіНЧСНБпЕФОрРыЯрЕШ
C. Ш§НЧаЮШ§ЬѕНЧЦНЗжЯпЕФНЛЕуЕНШ§ЬѕБпЕФОрРыЯрЕШ
D. вдЩЯОљВЛе§ШЗ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊдіМгЛЗБЃвтЪЖЃЌФГЩчЧјМЦЛЎПЊеЙвЛДЮЁАМѕЬМЛЗБЃЃЌМѕЩйгУГЕЪБМфЁБЕФаћДЋЛюЖЏЃЌЖдВПЗжМвЭЅЮхдТЗнЕФЦНОљУПЬьгУГЕЪБМфНјааСЫвЛДЮГщбљЕїВщЃЌВЂИљОнЪе МЏЕФЪ§ОнЛцжЦСЫШчЭМЫљЪОЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК

(1)БОДЮГщбљЕїВщСЫЖрЩйИіМвЭЅЃП
(2)НЋЭМЂйжаЕФЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
(3)ЧѓгУГЕЪБМфдк 1 аЁЪБЁЋ1.5 аЁЪБЕФВПЗжЖдгІЕФЩШ аЮдВаФНЧЕФЖШЪ§ЃЛ
(4)ШєИУЩчЧјгаГЕМвЭЅга 1 600 ИіЃЌЧыФуЙРМЦИУЩчЧјгУГЕЪБМфВЛГЌЙ§ 1.5 аЁЪБЕФдМгаЖрЩйИіМвЭЅЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
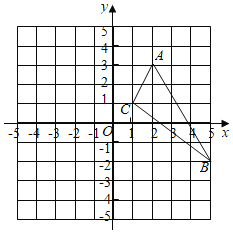
ЁОЬтФПЁПвбжЊШчЭМЃЌдк![]() жаЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ
жаЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ![]() ЃЌНЋ
ЃЌНЋ![]() би
би ![]() жсИКЗНЯђЦНвЦ
жсИКЗНЯђЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйби
ИіЕЅЮЛГЄЖШЃЌдйби![]() жсИКЗНЯђЦНвЦ
жсИКЗНЯђЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌЕУЕН
ИіЕЅЮЛГЄЖШЃЌЕУЕН![]() ЃЌЦф жаЕу
ЃЌЦф жаЕу![]() ЕФЖдгІЕуЮЊЕу
ЕФЖдгІЕуЮЊЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФЖдгІЕуЮЊЕу
ЕФЖдгІЕуЮЊЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФЖдгІЕуЮЊЕу
ЕФЖдгІЕуЮЊЕу![]()
![]() жБНгаДГіЦНвЦКѓЕФ
жБНгаДГіЦНвЦКѓЕФ![]() ЕФЖЅЕузјБъЃК
ЕФЖЅЕузјБъЃК
![]()
![]()
![]()
![]() дкзјБъЯЕжаЛГіЦНвЦКѓЕФ
дкзјБъЯЕжаЛГіЦНвЦКѓЕФ![]()
![]() ЧѓГі
ЧѓГі![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com