
【题目】请你根据如图所示的阿宝与仙鹤的对话,解答下列问题:
(1)仙鹤为什么说多边形内角和的度数不可能是![]() ;
;
(2)若图中仙鹤所提到的外角的度数为![]() ,请分别求仙鹤所画的多边形的内角和的度数与边数.
,请分别求仙鹤所画的多边形的内角和的度数与边数.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某工厂对零件进行检测,引进了检测机器.已知一台检测机的工作效率相当于一名检测员的20倍.若用这台检测机检测900个零件要比15名检测员检测这些零件少3小时.
(1)求一台零件检测机每小时检测零件多少个?
(2)现有一项零件检测任务,要求不超过7小时检测完成3450个零件.该厂调配了2台检测机和30名检测员,工作3小时后又调配了一些检测机进行支援,则该厂至少再调配几台检测机才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为边长为6的等边三角形,D,E分别在边BC,AC上,且CD=CE=x,连接DE并延长至点F,使EF=AE,连接AF,CF.
(1)求证:△AEF为等边三角形;
(2)求证:四边形ABDF是平行四边形;
(3)记△CEF的面积为S,
①求S与x的函数关系式;
②当S有最大值时,判断CF与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场柜台销售每台进价分别为160元、120元的![]() 、
、![]() 两种型号的电器,下表是近两周的销售情况:
两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)求![]() 、
、![]() 两种型号的电器的销售单价;
两种型号的电器的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求![]() 种型号的电器最多能采购多少台?
种型号的电器最多能采购多少台?
(3)在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标满足:
的坐标满足:![]()
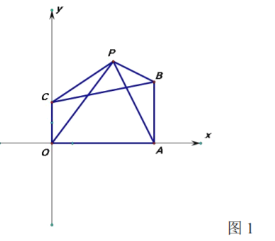
(1)求出点![]() 的坐标
的坐标
(2)如图1,连接![]() ,点
,点![]() 在四边形
在四边形![]() 外面且在第一象限,再连
外面且在第一象限,再连![]() ,则
,则![]() ,求
,求![]() 点坐标.
点坐标.
(3)如图2所示,![]() 为线段
为线段![]() 上一动点,
上一动点,![]() (在
(在![]() 右侧)为
右侧)为![]() 上一动点,使
上一动点,使![]() 轴始终平分
轴始终平分![]() ,连
,连![]() 且
且![]() ,那么
,那么![]() 是否为定值?若为定值,请直接写出定值,若不是,请简单说明理由.
是否为定值?若为定值,请直接写出定值,若不是,请简单说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com