
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 延长线上一点,点
延长线上一点,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)见解析;(2) 70°
【解析】
(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
(1)证明:∵∠ABC=90°,∴∠CBF=∠ABE=90°,
在Rt△ABE和Rt△CBF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)解:∵AB=BC,∠ABC=90°,∴∠CAB=∠ACB=45°,
又∵∠BAE=∠CAB﹣∠CAE=45°﹣20°=25°,由(1)知:Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=25°,∴∠ACF=∠BCF+∠ACB=45°+25°=70°.


科目:初中数学 来源: 题型:
【题目】已知,![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() .
.

(1)如图 1,若![]() ,求
,求![]() 的度数;
的度数;
(2)把“![]() °”改为“
°”改为“![]() ”,射线
”,射线![]() 沿射线
沿射线![]() 平移,得到
平移,得到![]() ,其它条件不变(如 图 2 所示),探究
,其它条件不变(如 图 2 所示),探究![]() 的数量关系;
的数量关系;
(3)在(2)的条件下,作![]() ,垂足为
,垂足为![]() ,与
,与![]() 的角平分线
的角平分线![]() 交于点
交于点![]() ,若
,若![]() , 用含 α 的式子表示
, 用含 α 的式子表示![]() (直接写出答案).
(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
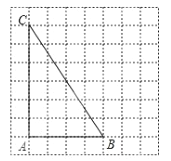
【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在![]() 上找一点P,使点P到
上找一点P,使点P到![]() 和
和![]() 的距离相等;
的距离相等;
②在射线![]() 上找一点Q,使
上找一点Q,使![]() .
.
(2)在(1)中连接![]() 与
与![]() ,试说明
,试说明![]() 是直角三角形.
是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了科学建设“学生健康成长工程”,随机抽取了部分学生家庭对其家长进行了主题“周末孩子在家您关心了吗?”的调查问卷,将收回的调查问卷进行了分析整理,得到了如下的样本统计图表和扇形统计图:
代号 | 情况分类 | 家庭数 |
A | 带孩子玩且关心其作业完成情况 | 8 |
B | 只关心其作业完成情况 | m |
C | 只带孩子玩 | 4 |
D | 既不带孩子玩也不关心其作业完成情况 | n |
(1)求m,n的值;
(2)该校学生家庭总数为500,学校决定按比例在B、C、D类家庭中抽取家长组成培训班,其比例为B类20%,C、D类各取60%,请你估计该培训班的家庭数;
(3)若在C类家庭中只有一个是城镇家庭,其余是农村家庭,请用列举法求出C类中随机抽出2个家庭进行深度家访,其中有一个是城镇家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你根据如图所示的阿宝与仙鹤的对话,解答下列问题:
(1)仙鹤为什么说多边形内角和的度数不可能是![]() ;
;
(2)若图中仙鹤所提到的外角的度数为![]() ,请分别求仙鹤所画的多边形的内角和的度数与边数.
,请分别求仙鹤所画的多边形的内角和的度数与边数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且![]() +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿平行于x轴的负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com