
 如图,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°,求:
如图,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°,求:分析 (1)利用“面积法”来求线段AD的长度;
(2)△AEC与△ABE是等底同高的两个三角形,它们的面积相等;
(3)由于AE是中线,那么BE=CE,于是△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE),化简可得△ACE的周长-△ABE的周长=AC-AB,易求其值.
解答 解:∵∠BAC=90°,AD是边BC上的高,
∴$\frac{1}{2}$AB•AC=$\frac{1}{2}$BC•AD,
∴AD=$\frac{AB•AC}{BC}=\frac{6×8}{10}$=4.8(cm),即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴$\frac{1}{2}$BE•AD=$\frac{1}{2}$EC•AD,即S△ABE=S△AEC,
∴S△ABE=$\frac{1}{2}$S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),即△ACE和△ABE的周长的差是2cm.
点评 本题考查了中线的定义、三角形周长的计算.解题的关键是利用三角形面积的两个表达式相等,求出AD.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:选择题
| A. | 3a2b-a2b=2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
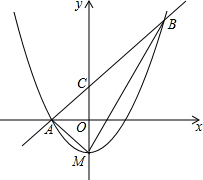 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com