
 (1)阅读合作学习内容,解答其中的问题;
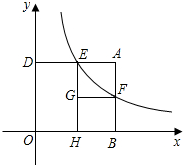
(1)阅读合作学习内容,解答其中的问题; | 合作学习 如图所示,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数 的图象分别相交于点E,F,且DE=2,过点E作EH⊥轴于点H,过点F作FG⊥EH于点G.回答下列问题: ①该反比例函数的解析式是什么? ②当四边形AEGF为正方形时,点F的坐标是多少? |
| 6 |
| x |
| AE |
| AF |
| OD |
| DE |
| 3 |
| 2 |
| 5 |
| 2 |
| 6 |
| x |
| 6 |
| x |
| 6 |
| x |
| AE |
| AF |
| OD |
| DE |
| 3 |
| 2 |
| 6 |
| x |
| 5 |
| 6 |
| 5 |
| 2 |
| AE |
| OD |
| ||
| 3 |
| 5 |
| 6 |


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.
用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:
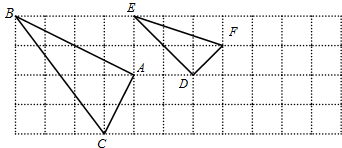
 如图,方格纸上的每个小方格都是边长为1 的正方形,△ABC的顶点均在格点上,若B点的坐标为(-4,-2)按要求回答下列问题
如图,方格纸上的每个小方格都是边长为1 的正方形,△ABC的顶点均在格点上,若B点的坐标为(-4,-2)按要求回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,轮船在A处观测到北偏东45°方向上有个灯塔B,轮船在正东方向20海里1.5小时后到达C处,又观测到灯塔B在北偏东30°方向上,则此时轮船与灯塔B相距海里.(结果保留根号)
如图所示,轮船在A处观测到北偏东45°方向上有个灯塔B,轮船在正东方向20海里1.5小时后到达C处,又观测到灯塔B在北偏东30°方向上,则此时轮船与灯塔B相距海里.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 11 | 2 | -1 | 2 | 5 | … |
| A、-2 | B、-1 | C、1 | D、2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com