
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
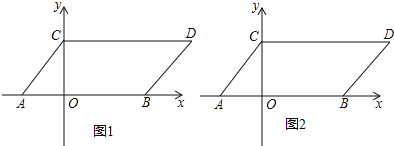
(1)写出点C,D的坐标并求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由;
(3)如图2,点P是直线BD上的一个动点,连接PC,PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD,∠POB的数量关系.
【答案】(1)C(0,2),D(4,2).8;(2)F(1,0)或(5,0);(3)当点P在线段BD上运动时:∠OPC=∠PCD+∠POB;当点P在BD延长线上运动时:∠OPC=∠POB-∠PCD;当点P在DB延长线上运动时:∠OPC=∠PCD-∠POB.
【解析】试题分析:(1)根据点平移的规律易得点C的坐标为(0,2),点D的坐标为(4,2);四边形ABDC的面积=2×(3+1)=8;
(2)存在.设点P到AB的距离为h,则S△PAB=![]() ×AB×h,根据S△PAB=S四边形ABDC,列方程求h的值,确定P点坐标.
×AB×h,根据S△PAB=S四边形ABDC,列方程求h的值,确定P点坐标.
(3)分类讨论:当点P在线段BD上,作PM∥AB,根据平行线的性质由MP∥AB得∠2=∠POB,由CD∥AB得到CD∥MF,则∠1=∠PCD,所以∠OPC=∠POB+∠PCD;同样得到当点P在线段DB的延长线上,∠OPC=∠PCD-∠POB;当点P在线段BD的延长线上,得到∠OPC=∠POB-∠PCD.
试题解析:(1)依题意,得C(0,2),D(4,2),
∴S四边形ABDC=AB×OC=4×2=8;
(2)在y轴上是否存在一点P,使S△PAB=S四边形ABDC.理由如下:
设点P到AB的距离为h,
S△PAB=![]() ×AB×h=2h,
×AB×h=2h,
由S△PAB=S四边形ABDC,得2h=8,
解得h=4,
∴P(0,4)或(0,-4).
(3)当点P在线段BD上,作PM∥AB,如图1,
∵MP∥AB,
∴∠2=∠POB,
∵CD∥AB,
∴CD∥MP,
∴∠1=∠PCD,
∴∠OPC=∠1+∠2=∠POB+∠PCD;
当点P在线段DB的延长线上,作PN∥AB,如图2,
∵PN∥AB,
∴∠NPO=∠POB,
∵CD∥AB,
∴CD∥PN,
∴∠NPC=∠FCD,
∴∠OPC=∠NPC-∠NPO=∠FCD-∠POB;
同样得到当点P在线段BD的延长线上,得到∠OPC=∠POB-∠PCD.



科目:初中数学 来源: 题型:
【题目】(2016广东省梅州市第22题)
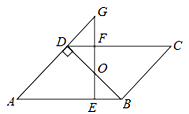
如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 有理数和无理数统称为实数 B. 实数是由正实数和负实数组成
C. 实数都可以表示在数轴上 D. 实数和数轴上的点一一对应
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆地上最高处是珠穆朗玛峰顶,高出海平面8848m,记为+8848m;陆地上最低处是地处亚洲西部的死海,低于海平面约415m,记为( )
A. +415m B. ﹣415m C. ±415m D. ﹣8848m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若―3xayzb与6x3ycz2是同类项,则a、b、c的值分别是( ).
A. a=1 b=2 c=3 B. a=3 b=1 c=2
C. a=3 b=2 c=1 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )
A.∠A=80°,∠D=100°
B.∠A=100°,∠D=80°
C.∠B=80°,∠D=80°
D.∠A=100°,∠D=100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com