Question

【题目】如图，在△ABC中，AB＝AC，AD为边BC上的中线，点E在AD上，以点A为圆心，AB长为半径画弧，交BE的延长线于点F，点G在EF上，且∠EAG＝∠CAF，连接CE．

（1）依题意补全图形；

（2）求证：FG＝CE；

（3）若EF平分∠AEC，则∠BAE与∠ABE满足的等量关系为　 　．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）∠BAE+∠ABE＝60°．

【解析】

（1）依题意补全图形即可；（2）由等腰三角形的性质得出∠ABE＝∠AFG，∠EAB＝∠GAF，证明△EAB≌△GAF（ASA），得出BE＝FG，证明△EAB≌△EAC（SAS），得出BE＝CE，即可得出结论；（3）由（2）得∠CAE＝∠BAE，△EAB≌△GAF，△EAB≌△EAC，由全等三角形的性质得出AE＝AG，∠ABE＝∠ACE，由等腰三角形的性质得出∠AEG＝∠AGE，证出∠AEG＝∠EAG＝∠AGE，得出△AGE是等边三角形，由等边三角形的性质得出∠AEG＝60°，由三角形的外角性质即可得出结论．

（1）解：依题意补全图形，如图所示：

（2）证明：由题意得：AB＝AC＝AF，

∴∠ABE＝∠AFG，

∵∠EAC+∠CAG＝∠EAG，∠CAG+∠GAF＝∠CAF，∠EAG＝∠CAF，

∴∠EAC＝∠GAF，

∵AB＝AC，AD为边BC上的中线，

∴∠EAC＝∠EAB，

∴∠EAB＝∠GAF，

在△EAB和△GAF中，，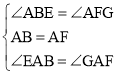

∴△EAB≌△GAF（ASA），

∴BE＝FG，

在△EAB和△EAC中，，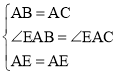

∴△EAB≌△EAC（SAS），

∴BE＝CE，

∴FG＝CE；

（3）解：由（2）得：∠CAE＝∠BAE，△EAB≌△GAF，△EAB≌△EAC，

∴AE＝AG，∠ABE＝∠ACE，

∴∠AEG＝∠AGE，

∵EF平分∠AEC，

∴∠AEG＝∠CEG，

∴∠AGE＝∠CEG，

∴AG∥CE，

∴∠GAC＝∠ACE，

∴∠ABE＝∠GAC，

∵∠AEG＝∠ABE+∠BAE，∠EAG＝∠EAC+∠GAC，

∴∠AEG＝∠EAG＝∠AGE，

∴△AGE是等边三角形，

∴∠AEG＝60°，

∴∠BAE+∠ABE＝60°，

故答案为：∠BAE+∠ABE＝60°．