
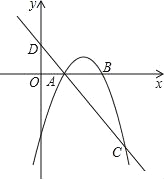
【题目】如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
(1)求抛物线解析式;
(2)点M是(1)中抛物线上一个动点,且位于直线AC的上方,试求△ACM的最大面积以及此时点M的坐标;
(3)抛物线上是否存在点P,使得△PAC是以AC为直角边的直角三角形?如果存在,求出P点的坐标;如果不存在,请说明理由.
【答案】(1)y=-x2+4x-3;(2)![]() ,M(
,M(![]() ,
,![]() );(3)(-1,-8)或(2,1).
);(3)(-1,-8)或(2,1).
【解析】
试题分析:(1)代入A,C两点,列出方程,解得a,b即可;
(2)设M(a,-a2+4a-3),求出直线直线AC的解析式为:y=1-x,过M作x轴的垂线交AC于N,则N(a,1-a),即有三角形ACM的面积为△AMN和△CMN的面积之和,化简运用二次函数的最值,即可得到;
(3)讨论当∠ACP=90°,当∠CAP=90°,运用直线方程和抛物线方程求交点即可.
试题解析:(1)由于A点的坐标是(1,0),C点坐标是(4,-3),
则a+b-3=0,且16a+4b-3=-3,
解得,a=-1,b=4,
即抛物线的解析式为:y=-x2+4x-3;
(2)设M(a,-a2+4a-3),
设直线AC的解析式为y=kx+b,
根据题意得:![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=1-x,
过M作x轴的垂线交AC于N,
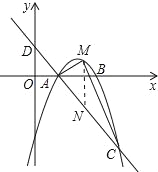
如图所示:则N(a,1-a),
即有三角形ACM的面积为△AMN与△CMN的面积之和,即为
![]() (a-1+4-a)(-a2+4a-3-1+a)
(a-1+4-a)(-a2+4a-3-1+a)
=![]() (-a2+5a-4),
(-a2+5a-4),
当a=![]() 时,面积取得最大,且为
时,面积取得最大,且为![]() ,
,
此时M(![]() ,
,![]() );
);
(3)存在,理由如下:
当∠ACP=90°,即有此时CP:y=x-7,
由CP解析式和抛物线解析式得: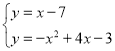 ,
,
解得:![]() ,或
,或![]() (不合题意舍去),
(不合题意舍去),
∴P(-1,-8);
当∠CAP=90°,由AC的斜率为-1,即有AP的斜率为1,
此时AP:y=x-1,
由AP解析式和抛物线解析式得: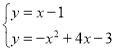 ,
,
解得:![]() ,或
,或![]() ,(不合题意舍去),
,(不合题意舍去),
∴P(2,1).
故存在点P,且为(-1,-8)或(2,1),使得△PAC是以AC为直角边的直角三角形.


科目:初中数学 来源: 题型:
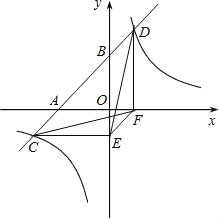
【题目】 如图,一次函数y=x+3的图象与x轴,y轴交于A,B两点,与反比例函数![]() 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④AC=BD.
其中正确的结论是( )
A.①② B.①②③
C.①②③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
A. (x+4)2=﹣7 B. (x+4)2=﹣9 C. (x+4)2=7 D. (x+4)2=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )
A. 2,2,4B. 3,2,6C. 1,2,2D. 1,2,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何模型:
条件:如图,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连结A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
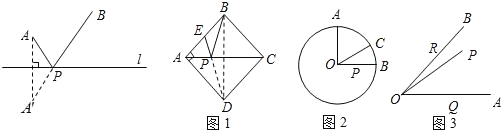
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则PB+PE的最小值是 ;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面现象能说明“面动成体”的是( )
A. 旋转一扇门,门运动的痕迹
B. 扔一块小石子,小石子在空中飞行的路线
C. 天空划过一道流星
D. 时钟秒针旋转时扫过的痕迹
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com