
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() 平分
平分![]() ,点
,点![]() 是
是![]() 上一点,以
上一点,以![]() 为直径的
为直径的![]() 经过点
经过点![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() 的面积
的面积![]() 的面积
的面积![]() ,
,![]() ,求
,求![]() 的长.
的长.
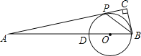
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连结OP,如图,由BP平分∠ABC得∠CBP=∠OBP,由OB=OP得∠OBP=∠OPB,则∠CBP=∠OPB,根据平行线的判定得OP∥BC,则利用平行线的性质得到∠APO=∠C=90°,于是可根据切线的判定定理得到结论;
(2)根据三角形面积公式由△ABP的面积-△BPC的面积=2可得BC(PA-1)=4,即BC=![]() ,再根据平行线分线段成比例定理可推出
,再根据平行线分线段成比例定理可推出![]() ,则AB=PABC,接着利用勾股定理有AB2=AC2+BC2,所以PA2BC2=(AP+1)2+BC2,移项变形得到(AP+1)2=BC2(PA2-1),所以PA+1=BC2(PA-1),然后把BC=
,则AB=PABC,接着利用勾股定理有AB2=AC2+BC2,所以PA2BC2=(AP+1)2+BC2,移项变形得到(AP+1)2=BC2(PA2-1),所以PA+1=BC2(PA-1),然后把BC=![]() 代入得到关于PA的方程,然后解方程即可.
代入得到关于PA的方程,然后解方程即可.
![]() 证明:连结
证明:连结![]() ,如图,
,如图,

∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
![]() 解:∵
解:∵![]() 的面积
的面积![]() 的面积
的面积![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
而![]() ,
,
∴![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某超市的某种商品一周内每天的进价与售价信息和实际每天的销售量情况如图表所示:
进价与售价折线图(单位:元/斤)

实际销售量表(单位:斤)
日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
销售量 | 30 | 40 | 35 | 30 | 50 | 60 | 50 |
则下列推断不合理的是( )
A. 该商品周一的利润最小
B. 该商品周日的利润最大
C. 由一周中的该商品每天售价组成的这组数据的众数是4(元/斤)
D. 由一周中的该商品每天进价组成的这组数据的中位数是3(元/斤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
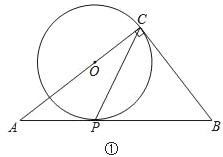
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
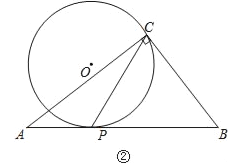
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
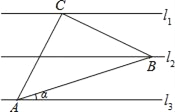
【题目】如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角三角形ABC的直角顶点C在l1上,另两个顶点A,B分别在l3,l2上,则sinα的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() .
.
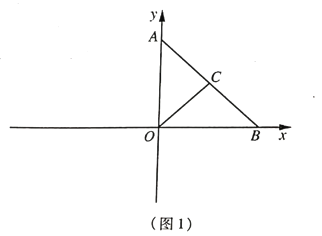
(1)如图1,求点![]() 的纵坐标;
的纵坐标;
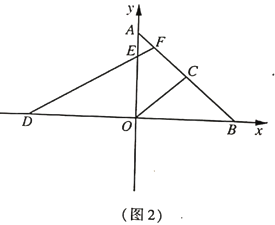
(2)如图2,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 在
在![]() 上,连接
上,连接![]() 交
交![]() 于点
于点![]() ;若
;若![]() ,求证:
,求证:![]()
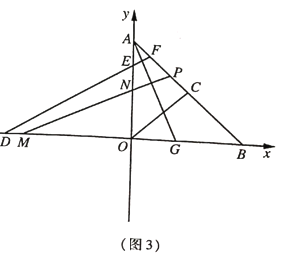
(3)如图3,在(2)的条件下,![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 与点
与点![]() 关于
关于![]() 轴对称,过点
轴对称,过点![]() 作
作![]() 分别交
分别交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com