
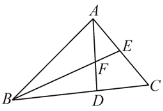
【题目】已知:如图,△ABC中,AD⊥BC于D,BE是三角形的角平分线,交AD于F.
(1)若∠ABC=40°, 求∠AFE的度数.
(2)若∠BAC是直角,请猜想:△AFE的形状,并写出证明.
【答案】(1)∠AFE=70°;(2)等腰三角形,证明见解析.
【解析】
(1)根据角平分线的定义求出∠DBF,再根据三角形内角和定理求出∠BFD即可解决问题.
(2)结论:△AEF是等腰三角形.想办法证明∠AEF=∠AFE即可.
(1)∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=40°,BE平分∠ABC,
∴∠DBF=![]() ∠ABC=20°,
∠ABC=20°,
∴∠BFD=90°-20°=70°
∴∠AFE=∠BFD=70°
(2)结论:△AEF是等腰三角形.
理由:∵∠BAE=∠ADB=90°,
∴∠AEF+∠ABE=90°,∠BFD+∠FBD=90°,
∵∠ABE=∠DBF,
∴∠AEF=∠BFD,
∵∠BFD=∠AFE,
∴∠AFE=∠AEF,
∴AE=AF,
∴△AEF是等腰三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OACB的顶点O、A、B的坐标分别是(0,0)、(0,a),(b,0),且a、b满足![]()
(1)如图1,求点C的坐标;
(2)如图2,点P为边OB上一动点,作等腰Rt△APD,且∠APD=90°.当点P从O运动到点B的过程中,求点D运动路程的长度;
(3)如图3,在(2)的条件下,作等腰Rt△BED,且∠DBE=90°,再作等腰Rt△ECF,且∠ECF=90°,直线FE分别交AC、OB于点M、N,求证:FM=EN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
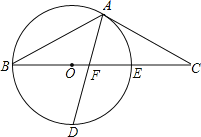
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径r.
,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接11.1—11.4义乌市森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数.下表提供了部分采购数据.
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DAB下列条件中不能使△ABC≌△ABD的是( )
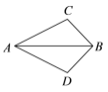
A. ∠C=∠D B. ∠ABC=∠ABD C. AC=AD D. BC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某小区开展了“节约用水为环保做贡献”的活动,为了解居民用水情况,在小区随机抽查了10户家庭的月用水量,结果如下表
月用水量(吨) | 8 | 9 | 10 |
户数 | 2 | 6 | 2 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A. 方差是4 B. 极差2 C. 平均数是9 D. 众数是9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=2016×2018-2016×2017, b=2015×2016-2013×2017,![]() ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A. a<b<c B. a<c<b C. b<a<c D. b<c<a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com