
【题目】为迎接11.1—11.4义乌市森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数.下表提供了部分采购数据.
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
【答案】(1)![]() ;(2)
;(2)![]() ;(3) 采购A产品15件
;(3) 采购A产品15件
时总利润最大,最大利润为10650元.
【解析】
(1)设y1与x的关系式y1=kx+b,由表列出k和b的二元一次方程,求出k和b的值,函数关系式即可求出;
(2)首先根据题意求出x的取值范围,结合x为整数,即可判断出商家的几种进货方案;
(3)令总利润为W,根据利润=售价-成本列出W与x的函数关系式W=30x2-540x+12000,把一般式写成顶点坐标式,求出二次函数的最值即可.
解:(1)设y1与x的关系式y1=kx+b,
由表知![]()
解得k=-20,b=1500,
即![]()
(2)根据题意可得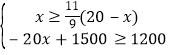
解得![]()
∵x为整数,
∴x可取的值为:11,12,13,14,15,
∴该商家共有5种进货方案;
(3)解法一:y2=-10(20-x)+1300=10x+1100,
令总利润为W,
则W=(1760-y1)x+(20-x)×[1700-(10x+1100)]=30x2-540x+12000,
=30(x-9)2+9570,
∵a=30>0,
∴当x≥9时,W随x的增大而增大,
∵11≤x≤15,
∴当x=15时,W最大=10650;
解法二:根据题意可得B产品的采购单价可表示为:
y2=-10(20-x)+1300=10x+1100,
则A、B两种产品的每件利润可分别表示为:
1760-y1=20x+260,
1700-y2=-10x+600,
则当20x+260>-10x+600时,A产品的利润高于B产品的利润,
即![]() 时,A产品越多,总利润越高,
时,A产品越多,总利润越高,
∵11≤x≤15,
∴当x=15时,总利润最高,
此时的总利润为(20×15+260)×15+(-10×15+600)×5=10650.
答:采购A种产品15件时总利润最大,最大利润为10650元.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )

A. 该班总人数为50人B. 步行人数为30人
C. 乘车人数是骑车人数的2.5倍D. 骑车人数占20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2017=( )
A. (31,51) B. (32,48) C. (33,47) D. (34,43)
查看答案和解析>>
科目:初中数学 来源: 题型:
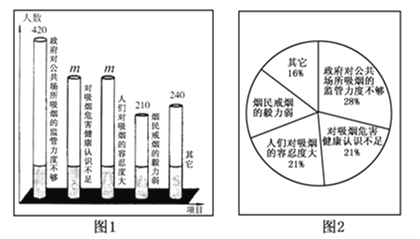
【题目】5月31日是世界无烟日,某卫生机构为了了解“导致吸烟人比例高的最主要原因”,随机抽样调查了该市部分18~65岁的市,民,下图是根据调查结果绘制的统计图,根据图中信息解答下列问题:
(1)这次接受随机抽样调查的市民总人数为 ;
(2)图1中m 的值是 ;
(3)求图2中认为“烟民戒烟的毅力弱”所对应的圆心角的度数;
(4)若该市18~65岁的市民约有200万人,请你估算其中认为导致吸烟人口比例高的最主要原因是“对吸烟危害健康认识不足”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
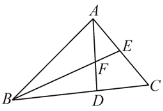
【题目】已知:如图,△ABC中,AD⊥BC于D,BE是三角形的角平分线,交AD于F.
(1)若∠ABC=40°, 求∠AFE的度数.
(2)若∠BAC是直角,请猜想:△AFE的形状,并写出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】耒阳市某校为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
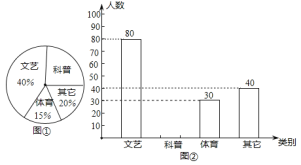
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为 ;
(2)补全条形图;
(3)求在扇形统计图中,喜欢“科普书籍”的所占的圆心角度数;
(4)如果全校共有学生1500名,请估计该校最喜欢“科普”书籍的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=2![]() ,∠AOB的平分线OC交AB于C,过O点作与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点作与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)当t=1时,求△CPQ的面积;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将点数为2,3,4的三张牌按从左到右的方式排列,并且按从左到右的牌面数字记录排列结果为234.现在做一个抽放牌游戏:从上述左、中、右的三张牌中随机抽取一张,然后把它放在其余两张牌的中间,并且重新记录排列结果.例如,若第1次抽取的是左边的一张,点数是2,那么第1次抽放后的排列结果是324;第2次抽取的是中间的一张,点数仍然是2,则第2次抽放后的排列结果仍是324.照此游戏规则,两次抽放后,这三张牌的排列结果仍然是234的概率为_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com