
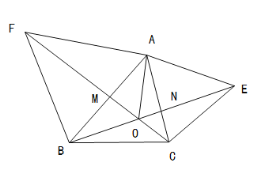
【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=2![]() ,∠AOB的平分线OC交AB于C,过O点作与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点作与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)当t=1时,求△CPQ的面积;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.

【答案】(1)OC=2,BC=2;(2)S△PQC=![]() ;(3)t为
;(3)t为![]() 或
或![]() 时,△OPM是等腰三角形.
时,△OPM是等腰三角形.
【解析】
(1)求出∠B,根据直角三角形性质求出OA,求出AB,在△AOC中,根据勾股定理得出关于OC的方程,求出OC即可;
(2)如图1﹣1中,作CH⊥PQ于H.当t=1时,P在BC上,Q在OC上,CQ=OQ=PC=PB=1,求出PQ,CH即可解决问题.
(3)有三种情况:①OM=PM时,求出OP=2OQ,代入求出即可;②PM=OP时,此时不存在等腰三角形;③OM=OP时,过P作PG⊥ON于G,求出OG和QG的值,代入OG+QG=t﹣2,即可求出答案.
解:(1)∵∠A=90°,∠AOB=60°,OB=2![]() ,
,
∴∠B=30°,
∴OA=![]() OB=
OB=![]() ,
,
由勾股定理得:AB=3,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°=∠B,
∴OC=BC,
在△AOC中,AO2+AC2=CO2,
∴(![]() )2+(3﹣OC)2=OC2,
)2+(3﹣OC)2=OC2,
∴OC=2=BC,
∴OC=2,BC=2.
(2)如图1﹣1中,作CH⊥PQ于H.当t=1时,P在BC上,Q在OC上,CQ=OQ=PC=PB=1,
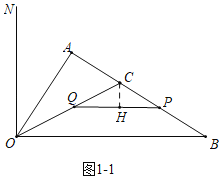
∴PQ∥OB,
∴∠CPQ=∠B=30°,
∵CQ=CP.CH⊥QP,
∴QH=PH,
∴CH=![]() PC=
PC=![]() ,QH=PH=
,QH=PH=![]() CH=
CH=![]() ,
,
∴QP=![]()
∴S△PQC=![]() PQCH=
PQCH=![]() ×
×![]() ×
×![]() =
=![]() .
.
(3)如图(2)所示:
∵ON⊥OB,
∴∠NOB=90°,
∵∠B=30°,∠A=90°,
∴∠AOB=60°,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°,
∴∠NOC=90°﹣30°=60°,
①OM=PM时,
∠MOP=∠MPO=30°,
∴∠PQO=180°﹣∠QOP﹣∠MPO=90°,
∴OP=2OQ,
∴2(t﹣2)=4﹣t,
解得:t=![]() ,
,
②PM=OP时,
此时∠PMO=∠MOP=30°,
∴∠MPO=120°,
∵∠QOP=60°,
∴此时不存在;
③OM=OP时,
过P作PG⊥ON于G,
OP=4﹣t,∠QOP=60°,
∴∠OPG=30°,
∴GO=![]() (4﹣t),PG=
(4﹣t),PG=![]() (4﹣t),
(4﹣t),
∵∠AOC=30°,OM=OP,
∴∠OPM=∠OMP=75°,
∴∠PQO=180°﹣∠QOP﹣∠QPO=45°,
∴PG=QG=![]() (4﹣t),
(4﹣t),
∵OG+QG=OQ,
∴![]() (4﹣t)+
(4﹣t)+![]() (4﹣t)=t﹣2,
(4﹣t)=t﹣2,
解得:t=![]() .
.
综合上述:当t为![]() 或
或![]() 时,△OPM是等腰三角形.
时,△OPM是等腰三角形.


科目:初中数学 来源: 题型:
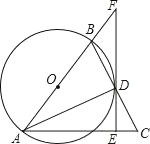
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,连接AD,过D作AC的垂线,交AC边于点E,交AB 边的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若∠F=30°,BF=3,求弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接11.1—11.4义乌市森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数.下表提供了部分采购数据.
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某小区开展了“节约用水为环保做贡献”的活动,为了解居民用水情况,在小区随机抽查了10户家庭的月用水量,结果如下表
月用水量(吨) | 8 | 9 | 10 |
户数 | 2 | 6 | 2 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A. 方差是4 B. 极差2 C. 平均数是9 D. 众数是9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,
(1)证明:CF=EB.
(2)证明:AB=AF+2EB.
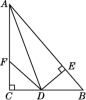
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
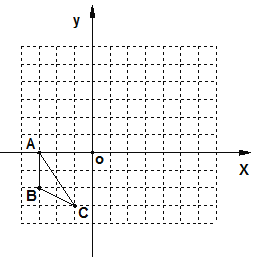
【题目】如图,在边长为1的正方形网格内有一个三角形ABC
(1)把△ABC沿着![]() 轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1
轴向右平移5个单位得到△A1B1C1,请你画出△A1B1C1
(2)请你以O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2,使得△ABC与△A2B2C2的位似比为1:2;
(3)请你写出△A2B2C2三个顶点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() 和
和![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)下列结论中,正确的有________个.
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() .
.
(3)请选择(2)中任一正确结论进行证明.你选的序号是 _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
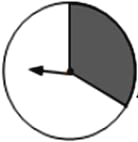
【题目】如图,转盘的白色扇形和黑色扇形的圆心角分别为240°和120°.让转盘自由转动2次,则指针一次落在白色区域,另一次落在黑色区域的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com