练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．

    （1）求证：AC=BD；

    （2）若大圆的半径R=10，小圆的半径r=8，且圆O到直线AB的距离为6，求AC的长．

    【答案】（1）证明见解析；（2）8﹣．

    【解析】

    试题（1）过O作OE⊥AB，根据垂径定理得到AE=BE，CE=DE，从而得到AC=BD；

    （2）由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，再根据勾股定理求出CE及AE的长，根据AC=AE﹣CE即可得出结论．

    试题解析：解：（1）证明：如答图，过点O作OE⊥AB于点E，

    ∵AE=BE，CE=DE，

    ∴BE﹣DE=AE﹣CE，即AC=BD.

    （2）由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，

    ∵OA=10，OC=8，OE=6，

    ∴.

    ∴AC=AE﹣CE=8﹣．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的三个顶点分别为A（－1，4），B（－5，3），C（－3，2）．

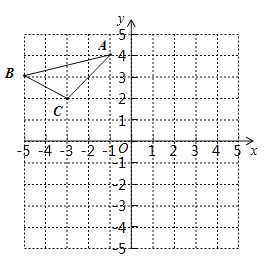
    （1）将△ABC向下平移6个单位后得到△A1B1C1，请在图中画出△A1B1C1，并写出C1点坐标；

    （2）图中点A2（1，2）与点A关于直线l成轴对称，请在图中画出直线l及△ABC关于直线l对称的△A2B2C2，并写出B2点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，牧童家在B处，A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m，天黑牧童从A处将牛牵到河边去饮水，在赶回家，那么牧童最少要走（ ）

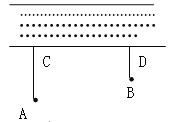
    A.800mB.1000mC.1200mD.1500m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为支援灾区建设，计划向、两受灾地运送急需物资分别为60吨和140吨，该市甲、乙两地有急需物资分别为120吨和80吨，已知甲、乙两地运到、两地的每吨物资的运费如表所示：

    甲

    乙

    20元/吨

    15元/吨

    25元/吨

    24元/吨

    （1）设甲地运到地的急需物资为吨，求总运费（元）关于（吨）的函数关系式，并写出的取值范围；

    （2）求最低总运费，并说明总运费最低时的运送方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y＝ax2＋bx＋c(a≠0)的部分图象，其顶点坐标为(1，n)，抛物线与x轴的一个交点在点(3，0)和(4，0)之间．则下列结论

    ①a－b＋c＞0；②3a＋b＝0；

    ③b2＝4a(c－n)；

    ④一元二次方程ax2＋bx＋c＝n－1有两个不相等的实数根．

    其中正确结论的个数是(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，OB=6cm，OC=8cm．求：

    （1）∠BOC的度数；

    （2）BE+CG的长；

    （3）⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知S△ABC＝12，AD平分∠BAC，且AD⊥BD于点D，则S△ADC的值是( )

    A. 10 B. 8 C. 6 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：

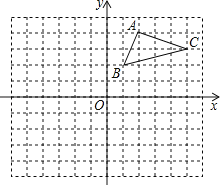
    （1）画出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标（　 ，　 ）；

    （2）将△ABC的三个顶点的横、纵坐标都乘以﹣1，分别得到对应点A2，B2，C2，请画出△A2B2C2，并说明△A1B1C1和△A2B2C2是否是轴对称图形，如果是，那么它们的对称轴是什么？如果不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东西方向的海岸线l上有一长为1km的码头MN（如图），在码头西端M的正西19.5km处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°，且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东60°，且与A相距km的C处．

    （1）求该轮船航行的速度（保留精确结果）；

    （2）如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．

    查看答案和解析>>

    同步练习册答案