
分析 (1)①延长DE交AB于F,根据平行线的性质求出∠DFA=∠D=40°,∠AED=∠A+∠DFA,代入求出即可;
②过E作EF∥AB,根据平行线的性质得出∠A=∠AEF,∠D=∠DEF,即可求出答案;
(2)根据题意画出符合的四种情况,根据图形和平行线的性质得出答案即可.
解答 (1)解:①延长DE交AB于F,如图1,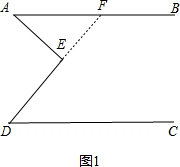
∵AB∥CD,∠D=40°,
∴∠DFA=∠D=40°,
∵∠A=20°,
∴∠AED=∠A+∠DFA=20°+40°=60°;
②∠AED=∠A+∠D,
证明:方法一、延长DE交AB于F,如图1,
∵AB∥CD,
∴∠DFA=∠D,
∴∠AED=∠A+∠DFA;
方法二、过E作EF∥AB,如图2,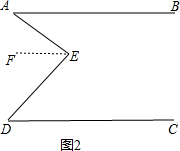
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A=∠AEF,∠D=∠DEF,
∴∠AED=∠AEF+∠DEF=∠A+∠D;
(2)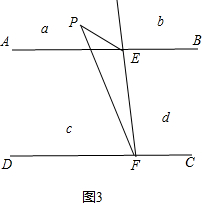
当P在a区域时,如图3,∠PEB=∠PFC+∠EPF;
当P点在b区域时,如图4,∠PFC=∠PEB+∠EPF;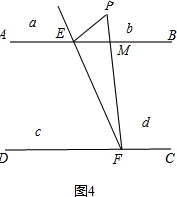
当P点在区域c时,如图5,∠EPF+∠PEB+∠PFC=360°;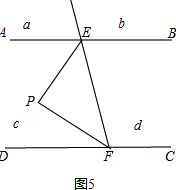
当P点在区域d时,如图6,∠EPF=∠PEB+∠PFC.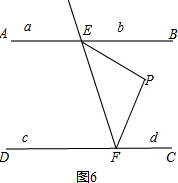
证明:图3,
∵AB∥CD,
∴∠PMB=∠PFC,
∵∠PMB=∠PEB+∠EPF,
∴∠PFC=∠PEB+∠EPF.
点评 本题考查了平行线的性质和判定,三角形外角性质的应用,能画出符合的各个情况是解此题的关键,用了分类讨论思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 第80个图形 | B. | 第82个图形 | C. | 第72个图形 | D. | 第95个图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
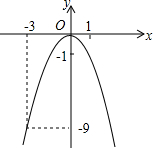 如图所示,从y=-x2的图象上可看出当-3<x≤1时,函数y的取值范围是( )
如图所示,从y=-x2的图象上可看出当-3<x≤1时,函数y的取值范围是( )| A. | -9<y≤-1 | B. | -9≤y<-1 | C. | -9≤y≤0 | D. | -9<y≤0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com