
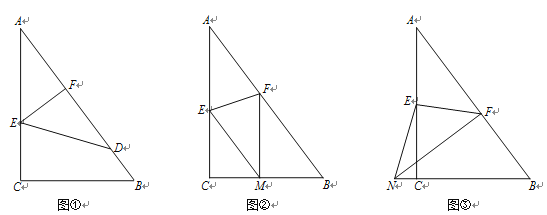
����Ŀ����ͼ����֪һ��ֱ��������ֽƬACB�����С�ACB��90�㣬AC��4��BC��3��E��F�ֱ���AC��AB���ϵ㣬����EF����ֽƬACB��һ����EF�۵���
��1����ͼ�٣����۵����A����AB���ϵĵ�D������ʹS�ı���ECBF��3S��AEF����AE�� ��
��2����ͼ�ڣ����۵����A����BC���ϵĵ�M������ʹMF��CA����AE�ij���
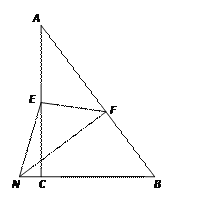
��3����ͼ�ۣ����۵����A����BC�ӳ����ϵĵ�N������ʹNF��AB����AE�ij���
���𰸡���1��AE��![]() ����2��
����2��![]() ����3��
����3��![]()
����������1��AE��![]() ��������������2��
��������������2��
��2����ͼ�ڣ���AE��x����CE��4��x��
�ߡ�ACB��90�㣬AC��4��BC��3����AB��5��
���۵���֪��AE��EM��x��AF��MF����AFE����MFE��
��MF��AC�����AEF����MFE�����AEF����AFE��
��AE��AF����AE��EM��MF��AF��
���ı���AEMFΪ���Σ�������������4��
��EM��AB�����CME�ס�CBA��������������5��
��![]() ��
��![]() ����
����![]() ��
��![]() �����x��
�����x��![]() ����AE��
����AE��![]() ������������6��
������������6��
��3����ͼ�ۣ���AE��y����CE��4��y��
���۵���֪��AE��EN��y��AF��NF��
��NF��AB�����NFB��90�㣮�ߡ�ACB��90�㣬���NFB����ACB��
 �ҡ�NBF����ABC�����NBF �ס�ABC��������������7��
�ҡ�NBF����ABC�����NBF �ס�ABC��������������7��
��![]() ��
��![]() ��
��![]() ����BF��
����BF��![]() NF��
NF��![]() AF����BF+ AF��AB��5��
AF����BF+ AF��AB��5��
��ã�BF��![]() ��NF��
��NF��![]() ��������������8��
��������������8��
��BN��![]() ��CN��BN��BC��
��CN��BN��BC��![]() ��3��
��3��![]() ��������������9��
��������������9��
![]() ��Rt��CEN����CN2+CE2��EN2����(
��Rt��CEN����CN2+CE2��EN2����(![]() )2+(4��y)2��y2��
)2+(4��y)2��y2��
��ã�y��![]() ����AE��
����AE��![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ����Ʒ�����˳������.��ͼ�Ǹ��ݳ�������IJ�Ʒ���أ���λ���ˣ����ݻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ�����в�Ʒ���صķ�Χ��[96��106]����96��������106�����������ݷ���Ϊ[96��98������96������<98���������ƣ�[98��100),[100��102)��[102��104),[104��106],��֪�����в�Ʒ����С��100�˵ĸ�����36���������о��ش��ڻ����98�˲���С��104�˵IJ�Ʒ�ĸ����� ( )
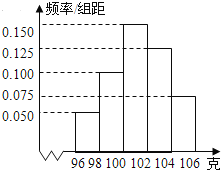
A. 90 B. 75 C. 60 D. 45
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ��� y ��ax+b��ͼ���� A (1,3)���� y ��2x��3 ƽ�У�
(1)��� a ��b .д�� y�� x�ĺ�����ϵ��
(2)�� x ����2 ʱ��y��ֵ���� y ��9ʱ��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�ֳ��ȵ�λ��1�ף�109���ף���֪ij��ֲ�ﻨ�۵�ֱ��ԼΪ35000���ף���ô�ÿ�ѧ��������ʾ���ֻ��۵�ֱ��Ϊ( )
A. 3.5��10��6��B. 3.5��10��5��C. 35��1013��D. 3.5��1013��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��6���µ�Ӥ�����������÷dz��죬���ǵ�����y(��)������x(��)��Ĺ�ϵ������y��a+700x����ʾ������a��Ӥ������ʱ�����أ�һ��Ӥ������ʱ��������3000�ˣ����Ӥ����4���µ�����Ϊ( )
A. 6000��B. 5800��C. 5000��D. 5100��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��Ϊƽ����һ��������������ͼ��ͼ��Ϊ��ʾ��ͼ��������AB������CD����ֱ�ڵ��棬BD��20m����A����D��ĸ���Ϊ45�㣬���C�������Ϊ58�㣮������CD�ĸ߶ȣ����ο����ݣ�sin58���0.85��cos58���0.53��tan58���1.60��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2006��¹����籭�������У�32֧����ӽ���Ϊ8��С����е�ѭ��������С������������£�ʤһ����3�֣�ƽһ����1�֣���һ����0�֣���С������ij�ӵĻ���Ϊ5�֣���öӱ��ǣ� ��
A.��ʤһ��
B.һʤ��ƽ
C.һʤһƽһ��
D.һʤ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У���A��ֱ��y��![]() x��
x��![]() ��һ���㣬����A����ƽ��1����λ�õ���B����C��1��0������
��һ���㣬����A����ƽ��1����λ�õ���B����C��1��0������
OB��CB����СֵΪ____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����a�ķ���2��a+2��=a+4�Ľ�Ҳ�ǹ���x�ķ���2��x��3����b=7�Ľ⣮
��1����a��b��ֵ��
��2�����߶�AB=a����ֱ��AB��ȡһ��P��ǡ��ʹ![]() =b����QΪPB���е㣬�뻭��ͼ�β�����߶�AQ�ij���
=b����QΪPB���е㣬�뻭��ͼ�β�����߶�AQ�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com