
【题目】已知四边形![]() 的一组对边
的一组对边![]() 的延长线相交于点
的延长线相交于点![]() .
.

(1)如图1,若![]() ,求证
,求证![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为6,求四边形
的面积为6,求四边形![]() 的面积;
的面积;
(3)如图3,另一组对边![]() 的延长线相交于点
的延长线相交于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的长(用含
的长(用含![]() 的式子表示).
的式子表示).
【答案】(1)证明见解析;(2)75-18![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)证明ΔEAB∽ΔECD,即可得解.
(2)过点C作CG⊥AD于点G,过点A作AH⊥BC于点H,在RtΔCDG中利用已知条件可求出DG、CG的长,再根据ΔCDE的面积为6,可求出ED的长,在ΔABH中可求出BH 、AH长,利用(1)可知ΔECG∽ΔEAH,从而可求出EH的长,利用S四边形ABCD=SΔAEH-SΔECG-SΔABH即可得解;
(3)由(1)(2)提供的思路即可求解.
试题解析:(1)∵∠ADC=90°
∴∠EDC=90°
∴∠ABE=∠CDE
又∵∠AEB=∠CED
∴ΔEAB∽ΔECD
∴![]()
∴![]()
(2) 过点C作CG⊥AD于点G,过点A作AH⊥BC于点H,
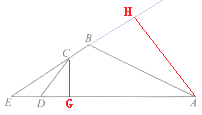
∵CD=5,cos∠ADC=![]()
∴DG=3,CG=4
∵SΔCED=6
∴ED=3
∴EG=6
∵AB=12 ∠ABC=120°
∴BH=6 AH=6![]()
由(1)有:ΔECG∽ΔEAH
∴![]()
∴EH=9![]()
∴S四边形ABCD=SΔAEH-SΔECG-SΔABH
=![]()
=75-18![]()
(3)![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2020年南充市各级各类学校学生人数约为1 150 000人,将1 150 000 用科学计数法表示为( )
A.1.15×106B.1.15×107C.11.5×105D.0.115×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于
的图象相交于![]() 和
和![]() 两点.
两点.
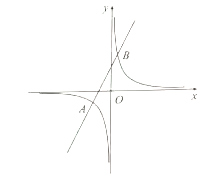
(1)求![]() 的值;
的值;
(2)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() .若
.若![]() ,求
,求![]() 的值;
的值;
(3)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,斜边
,斜边![]() 的两个端点分别在相互垂直的射线
的两个端点分别在相互垂直的射线![]() 上滑动,下列结论:
上滑动,下列结论:
①若![]() 两点关于
两点关于![]() 对称,则
对称,则![]() ;
;
②![]() 两点距离的最大值为
两点距离的最大值为![]() ;
;
③若![]() 平分
平分![]() ,则
,则![]() ;
;
④斜边![]() 的中点
的中点![]() 运动路径的长为
运动路径的长为![]() .
.
其中正确的是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com