
.如图,下列说法错误的是( )


A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
已知函数 ,若
,若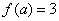 ,则
,则 .
.
分析:本题是分段函数的求值问题,考查 由函数值求自变量的值,对于此类问题的求解,只需对自变量属于那段定义域进行分类讨论,在相应的条件下将所得答案是否在对应的定义域内进行取舍,若在,则保留;否则相应的答案就要舍去.
由函数值求自变量的值,对于此类问题的求解,只需对自变量属于那段定义域进行分类讨论,在相应的条件下将所得答案是否在对应的定义域内进行取舍,若在,则保留;否则相应的答案就要舍去.
查看答案和解析>>
科目:初中数学 来源: 题型:
函数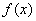 在
在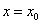 处导数存在,若
处导数存在,若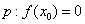 ;
;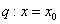 是
是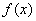 的极值点,则( )
的极值点,则( )
A. 是
是 的充分必要条件 B.
的充分必要条件 B.  是
是 的充分条件,但不是
的充分条件,但不是 的必要条件
的必要条件
C.  是
是 的必要条件,但不是
的必要条件,但不是 的充分条件 D.
的充分条件 D.  既不是
既不是 的充分条件,也不是
的充分条件,也不是 的必要条件
的必要条件
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2.其推理依据是( )
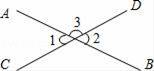

A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,EF∥AD,∠1=∠2,∠BAC=65°.将下面求∠AGD的过程填写完整.
解:∵EF∥AD(已知)
∴∠2= ( )
又∵∠1=∠2(已知)
∴∠1= (等量代换)
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=65°(已知)
∴∠AGD= .


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB、CD相交于点O,∠A=∠1,∠B=∠2,则∠C=∠D.理由是:
∵∠A=∠1,∠B=∠2,(已知)
且∠1=∠2( )
∴∠A=∠B.(等量代换)
∴AC∥BD( ).
∴∠C=∠D( ).


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com