
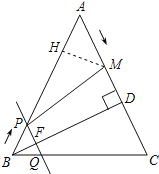
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��10cm��BD��AC�ڵ�D��BD��8cm����M�ӵ�A��������AC�ķ��������˶���ͬʱֱ��PQ�ɵ�B��������BA�ķ��������˶����˶�������ʼ�ձ���PQ��AC��ֱ��PQ��AB�ڵ�P����BC�ڵ�Q����BD�ڵ�F������PM�����˶�ʱ��Ϊt�루0��t��5�����߶�CM�ij��ȼ���y�����߶�BP�ij��ȼ���y����y����y������ʱ��t�ĺ����仯�����ͼ��ʾ��

��1����ͼ2��֪����M���˶��ٶ���ÿ���� cm����t���� ��ʱ���ı���PQCM��ƽ���ı��Σ���ͼ2�з�ӳ��һ����ĵ����� ����д���˵�����꣩��
��2�����ı���PQCM�����Ϊycm2����y��t֮��ĺ�����ϵʽ��
��3������PC���Ƿ����ijһʱ��t��ʹ��M���߶�PC�Ĵ�ֱƽ�����ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
���𰸡���1��2��![]() ��E��
��E��![]() ��
��![]() ������2��y��
������2��y��![]() t2��8t+40����3�����ڣ�t��
t2��8t+40����3�����ڣ�t��![]() sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�
sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�
��������
��1������ͼ2�жϳ���M���ٶ�Ϊ2cm/s��PQ���˶��ٶ�Ϊ1cm/s�������ı���PQCMΪƽ���ı��Σ�����ƽ���ı��ε����ʵõ��Ա�ƽ�У������õ�AP=AM���г�����t�ķ��̣�������̵Ľ�õ���������t��ֵ��
��2������PQ��AC�ɵ���PBQ�ס�ABC���������������ε���״��Ȼ��ͬ��֪��BPQҲΪ���������Σ���BP=PQ=t�����ú�t�Ĵ���ʽ�Ϳ��Ա�ʾ��BF�������õ����εĸ�PE=DF=8-t���ֵ�M���˶��ٶȺ�ʱ���֪��M�߹���·��AM=2t���������ε��µ�CM=10-2t�����������ε������ʽ���ɵõ�y��t�Ĺ�ϵʽ��
��3��������ڣ�����ݴ�ֱƽ�����ϵĵ㵽�߶����˵�ľ�����ȼ��ɵõ�MP=MC������M��MH��ֱAB����һ�Թ����ǵ���Ⱥ�һ��ֱ�ǵ���ȼ��ɵõ���AHM�ס�ADB�������Ƶõ���Ӧ�߳ɱ��������ú�t�Ĵ���ʽ��ʾ��AH��HM�ij�������AP�ij���AH�ij���ʾ��PH�ij����Ӷ���ֱ��������PHM�и��ݹ��ɶ�����ʾ��MP��ƽ��������AC�ij���AM�ij���ʾ��MC��ƽ�����������ߵ�����г�����t�ķ��̽������t��ֵ��
��1����ͼ2�ã���M���˶��ٶ�Ϊ2cm/s��PQ���˶��ٶ�Ϊ1cm/s��
���ı���PQCM��ƽ���ı��Σ���PM��QC��
��AP��AB��AM��AC��
��AB��AC��
��AP��AM����10��t��2t��
��ã�t��![]() ��
��
�൱t��![]() ʱ���ı���PQCM��ƽ���ı��Σ���ʱ��ͼ2�з�ӳ��һ����ĵ���E��
ʱ���ı���PQCM��ƽ���ı��Σ���ʱ��ͼ2�з�ӳ��һ����ĵ���E��![]() ��
��![]() ��
��
�ʴ�Ϊ��2��![]() ��E��
��E��![]() ��
��![]() ����
����
��2����PQ��AC��
���PBQ�ס�ABC��
���PBQ����������PQ��PB��t��
��![]() ����
����![]()
��ã�BF��![]() t��
t��
��FD��BD��BF��8��![]() t��
t��
�֡�MC��AC��AM��10��2t��
��y��![]() ��PQ+MC��FD��
��PQ+MC��FD��![]() ��t+10��2t����8��
��t+10��2t����8��![]() t����
t����![]() t2��8t+40��
t2��8t+40��
��3���������ijһʱ��t��ʹ��M���߶�PC�Ĵ�ֱƽ�����ϣ���MP��MC��
��M��MH��AB����AB��H����ͼ��ʾ��
�ߡ�A����A����AHM����ADB��90����
���AHM�ס�ADB��
��![]()
�֡�AD��6��
��![]()
��HM��![]() t��AH��
t��AH��![]() t��
t��
��HP��10��t��![]() t��10��
t��10��![]() t��
t��
��Rt��HMP��MP2����![]() t��2+��10��
t��2+��10��![]() t��2��
t��2��![]() t2��44t+100��
t2��44t+100��
�֡�MC2����10��2t��2��100��40t+4t2��
��MP2��MC2��
��![]() t2��44t+100��100��40t+4t2��
t2��44t+100��100��40t+4t2��
��� t1��![]() ��t2��0����ȥ����
��t2��0����ȥ����
��t��![]() sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�
sʱ����M���߶�PC�Ĵ�ֱƽ�����ϣ�


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������![]() ��������ԭ�㣮
��������ԭ�㣮
��1���������ߵĽ���ʽ�Ͷ���B�����ꣻ
��2�����A����������x�����һ��������A��C�������y��Գƣ�����y����ȷ��һ��P��ʹPA+PB��̣��������P�����ꣻ
��3������A��AD��BP��y���ڵ�D����ֱ��AP��AD��CP������ȵĵ�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽���ѧ���ԡ���ǿ���ԡ������ʶ��ߡ������й�ʫ�ʴ�ᡷ���������й��ˡ��ĸ����ӽ�Ŀ��ϲ������������ȡ��![]() ��ѧ�����е���ͳ��(Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ)���������������Ƴ���ͼͳ��ͼ����
��ѧ�����е���ͳ��(Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ)���������������Ƴ���ͼͳ��ͼ����
��Ŀ | ����(��) | �ٷֱ� |
��ǿ���� |
|
|
�ʶ��� |
|
|
�й�ʫ�ʴ�� |
|
|
������� |
|
|
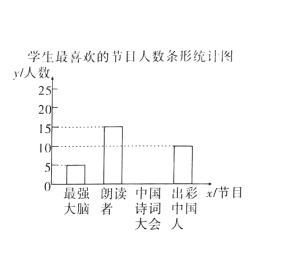
���������ṩ����Ϣ������������⣺
![]() ��
��![]() ��
��![]() ��
��
![]() ��ȫ���������ͳ��ͼ��
��ȫ���������ͳ��ͼ��
![]() ��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ
��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ![]() ��ͬѧ����ѧУ�μ�������֯�ľ���������������ȡ��
��ͬѧ����ѧУ�μ�������֯�ľ���������������ȡ��![]() ��ͬѧǡ����
��ͬѧǡ����![]() ����ͬѧ��
����ͬѧ��![]() ��Ůͬѧ�ĸ��ʣ�
��Ůͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
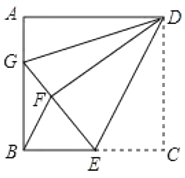
����Ŀ����ͼ��������![]() �У���
�У���![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() ����
����![]() ��
��![]() ������
������![]() ���ӳ�
���ӳ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ���������½��ۣ���
���������½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ������������ȷ���۵ĸ����ǣ� ��
������������ȷ���۵ĸ����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ҽԺ�ֱ���һ��һŮ��4��ҽ����Ա֧Ԯ�����人�������飮
(1)���Ӽס�����ҽԺ֧Ԯ��ҽ����Ա�зֱ����ѡ1��������ѡ��2��ҽ����Ա�Ա���ͬ�ĸ������� ������
(2)����֧Ԯ��4��ҽ����Ա�����ѡ2�������б�����״ͼ�ķ��������2��ҽ����Ա����ͬһ��ҽԺ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
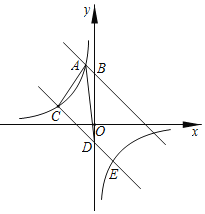
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��y�ύ�ڵ�![]() ���뷴��������
���뷴��������![]() �ڵڶ������ڵ�ͼ���ཻ�ڵ�
�ڵڶ������ڵ�ͼ���ཻ�ڵ�![]() ��
��
��1����ֱ��AB�Ľ���ʽ��
��2����ֱ��AB����ƽ��9����λ���뷴����������ͼ���ڵ�C�͵�E����y�ύ�ڵ�D����![]() �������
�������
��3����ֱ��CD�Ľ���ʽΪ![]() ������ͼ��ֱ��д������ʽ
������ͼ��ֱ��д������ʽ![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���ų�Ա��������ѧ��֪ʶ����ij����ƵĿ���![]() ͼ���߶�MN�ij�
ͼ���߶�MN�ij�![]() ��ֱ��MN��ֱ�ڵ��棬����Ϊ��
��ֱ��MN��ֱ�ڵ��棬����Ϊ��![]() �ڵ���A����õ�M������Ϊ
�ڵ���A����õ�M������Ϊ![]() ����N������Ϊ
����N������Ϊ![]() ����B����õ�M������Ϊ
����B����õ�M������Ϊ![]() ��
��![]() �ף���A��B��P������һֱ����
�ף���A��B��P������һֱ����![]() ������������������ƵĿ�MN�ij���
������������������ƵĿ�MN�ij���
![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
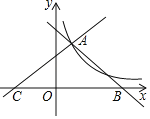
����Ŀ����ͼֱ��y1����x+4��y2��![]() x+b����˫����y��
x+b����˫����y��![]() ���ڵ�A(1��3)��������ֱ�߷ֱ���x�ύ��B��C���㣮
���ڵ�A(1��3)��������ֱ�߷ֱ���x�ύ��B��C���㣮
��1����k��ֵ��
��2��ֱ��д����x��0ʱ������ʽ![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
��3������P��x���ϣ�����AP����AP�ѡ�ABC������ֳ�1��2�����֣����ʱ��P���������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC�ǡ�O��ֱ����AB�ǡ�O��һ���ң�AP�ǡ�O�����ߣ���BM��AB����AP���ڵ� M���ӳ�MB��AC�ڵ�E������O�ڵ�D������AD��BC��
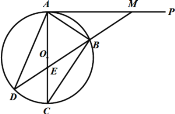
��1����֤��AB��BE��
��2����BE��3��OC��![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com