
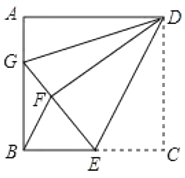
【题目】如图,正方形![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .给出以下结论:①
.给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据正方形的性质和折叠的性质可得AD=DF,∠A=∠GFD=90°,于是根据“HL”判定Rt△ADG≌Rt△FDG,可判断①的正误;设正方形ABCD的边长为a,AG=FG=x,BG=ax,根据勾股定理得到x=![]() a,得到BG=2AG,故②正确;根据已知条件得到△BEF是等腰三角形,易知△GED不是等腰三角形,于是得到△EBF与△DEG不相似,故③错误;连接CF,根据三角形的面积公式得到S△BFC=2S△BEF.故④错误.
a,得到BG=2AG,故②正确;根据已知条件得到△BEF是等腰三角形,易知△GED不是等腰三角形,于是得到△EBF与△DEG不相似,故③错误;连接CF,根据三角形的面积公式得到S△BFC=2S△BEF.故④错误.
解:如图,由折叠和正方形性质可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
在Rt△ADG和Rt△FDG中,
![]() ,
,
∴Rt△ADG≌Rt△FDG(HL),故①正确;
设正方形ABCD的边长为a,AG=FG=x,BG=ax,
∵BE=EC,
∴EF=CE=BE=![]() a
a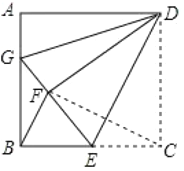
∴GE=![]() a+x
a+x
由勾股定理得:EG2=BE2+BG2,
即:(![]() a+x)2=(
a+x)2=(![]() a)2+(a-x)2解得:x=
a)2+(a-x)2解得:x=![]()
∴BG=2AG,
故②正确;
∵BE=EF,
∴△BEF是等腰三角形,易知△GED不是等腰三角形,
∴△EBF与△DEG不相似,
故③错误;
连接CF,
∵BE=CE,
∴BE=![]() BC,
BC,
∴S△BFC=2S△BEF.
故④错误,
综上可知正确的结论的是2个.
故选:B.


科目:初中数学 来源: 题型:
【题目】为了了解青少年形体情况,现随机抽查了某市若十名初中学生坐必、站姿.走安的好坏情况我们对测评数据作了适当处理(如果一个学生有一种以上:不良姿势.以他最突出的一种作记载) ,并将统计结果绘制了如下两幅不完整的统计图.请你根据图中所给信息解答下列问题:
![]() 求这次抽查一共抽查了多少名学生;
求这次抽查一共抽查了多少名学生;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 如果全市有
如果全市有![]() 万名初中生,那么全市初中生中,三姿良好的学生约有多少名
万名初中生,那么全市初中生中,三姿良好的学生约有多少名

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
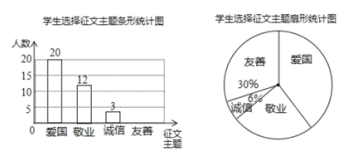
(1)求本次调查共抽取了多少名学生的征文;
(2)将上面的条形统计图和扇形统计图补充完整;
(3)本次抽取的3份以“诚信”为主题的征文分别是小义、小玉和大力的,若从中随机选取2份以“诚信”为主题的征文进行交流,请用画树状图法或列表法求小义和小玉同学的征文同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
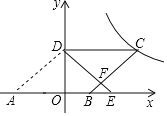
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y![]() (k≠0)图象经过点C,且S△BEF=1,则k的值为________.
(k≠0)图象经过点C,且S△BEF=1,则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
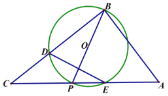
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
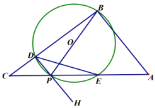
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x铀的一个交点在点(3,0)和(4,0)之间,则下列结论:①abc>0;②a﹣b+c>0;③b2=4a(c﹣m);④一元二次方程ax2+bx+c=m+1有两个不相等的实数根,其中正确结论的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,同时直线PQ由点B出发,沿BA的方向匀速运动,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t≤5).线段CM的长度记作y甲,线段BP的长度记作y乙,y甲和y乙关于时间t的函数变化情况如图所示.

(1)由图2可知,点M的运动速度是每秒 cm;当t= 秒时,四边形PQCM是平行四边形?在图2中反映这一情况的点是 (并写出此点的坐标);
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
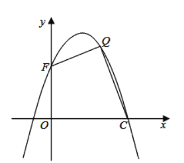
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()

(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小组做用频率估计概率“的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 掷一枚均匀的正六面体骰子,出现3点朝上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com