
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y![]() (k≠0)图象经过点C,且S△BEF=1,则k的值为________.
(k≠0)图象经过点C,且S△BEF=1,则k的值为________.
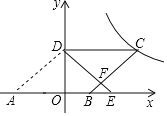
【答案】24
【解析】
连接OC,BD,根据折叠的性质得到OA=OE,得到OE=2OB,求得OA=2OB,设OB=BE=x,则OA=2x,根据平行四边形的性质得到CD=AB=3x,根据相似三角形的性质得到![]() ,求得S△BDF=3,S△CDF=9,于是得到结论.
,求得S△BDF=3,S△CDF=9,于是得到结论.
解:如图,连接OC,BD,
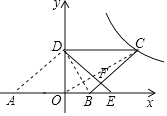
∵将△AOD沿y轴翻折,使点A落在x轴上的点E处,
∴OA=OE,
∵点B恰好为OE的中点,
∴OE=2OB,
∴OA=2OB,
设OB=BE=x,则OA=2x,
∴AB=3x,
∵四边形ABCD是平行四边形,
∴CD=AB=3x,
∵CD∥AB,
∴△CDF∽△BEF,
∴![]() ,
,
∵S△BEF=1,
∴S△BDF=3,S△CDF=9,
∴S△BCD=12,
∴S△CDO=S△BDC=12,
∴k的值=2S△CDO=24.


科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学综合实践课上,老师提出问题:如图,有一张长为![]() ,宽为
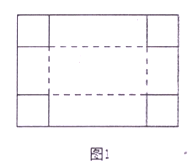
,宽为![]() 的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
(1)设小正方形的边长为![]() ,长方体体积为
,长方体体积为![]() ,根据长方体的体积公式,可以得到
,根据长方体的体积公式,可以得到![]() 与
与![]() 的函数关系式是 ,其中自变量
的函数关系式是 ,其中自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)列出![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
(注:补全表格,保留1位小数点)
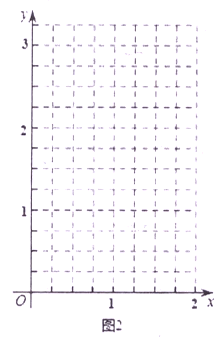
(3)如图,请在平面直角坐标系中描出以补全后表格中各对对应值为坐标的点,画出该函数图象;
(4)结合函数图象回答:当小正方形的边长约为 ![]() 时,无盖长方体盒子的体积最大,最
时,无盖长方体盒子的体积最大,最
大值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠BDC=30°,DC=4,AE⊥BD于E,CF⊥BD于F,且E、F恰好是BD的三等分点,AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
节目 | 人数(名) | 百分比 |
最强大脑 |
|
|
朗读者 |
|
|
中国诗词大会 |
|
|
出彩中国人 |
|
|
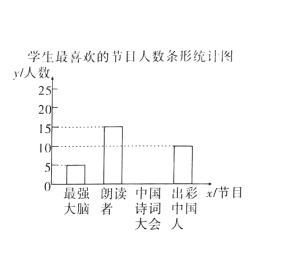
根据以上提供的信息.解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 补全上面的条形统计图;
补全上面的条形统计图;
![]() 名女同学.其余为男同学,现要从中随机抽取
名女同学.其余为男同学,现要从中随机抽取![]() 名同学代表学校参加市里组织的竞赛活动,请求出所抽取的
名同学代表学校参加市里组织的竞赛活动,请求出所抽取的![]() 名同学恰好是
名同学恰好是![]() 名男同学和
名男同学和![]() 名女同学的概率.
名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
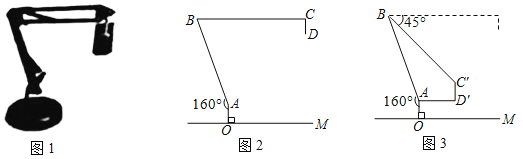
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
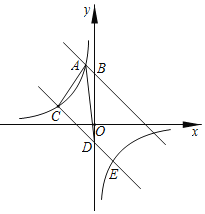
【题目】如图,在平面直角坐标系中,直线AB与y轴交于点![]() ,与反比例函数
,与反比例函数![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() .
.
(1)求直线AB的解析式;
(2)将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E,与y轴交于点D,求![]() 的面积;
的面积;
(3)设直线CD的解析式为![]() ,根据图象直接写出不等式
,根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 上的四个点,连接
上的四个点,连接![]() 交
交![]() 于点
于点![]()
![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交直线
交直线![]() 于点
于点![]()
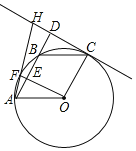
(1)判断四边形![]() 的形状并说明理由;
的形状并说明理由;
(2)求证:![]() 是
是![]() 的切线:
的切线:
(3)若![]() 求
求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com