
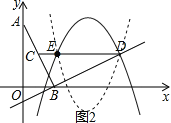
【题目】如图,O为原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,连结CD,某抛物线y=ax2+bx+c(a≠0)经过点D、点E(1,1).
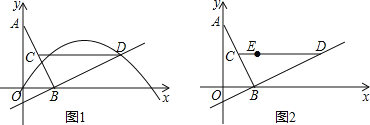
(1)若该抛物线过原点O,则a= ;
(2)若点Q在抛物线上,且满足∠QOB与∠BCD互余,要使得符合条件的Q点的个数是4个,则a的取值范围是 .
【答案】(1)﹣![]() ;(2)a<﹣
;(2)a<﹣![]() 或a>
或a>![]() .
.
【解析】
试题分析:(1)过点D作DF⊥x轴于点F,先通过三角形全等求得D的坐标,把D、E的坐标和c=0代入y=ax2+bx+c,根据待定系数法即可求得;
(2)若符合条件的Q点的个数是4个,则当a<0时,抛物线交于y轴的负半轴,当a>0时,抛物线与直线OQ:y=﹣![]() x有两个交点,得到方程ax2﹣4ax+3a+1=﹣
x有两个交点,得到方程ax2﹣4ax+3a+1=﹣![]() x,根据根与系数的关系得出不等式,解不等式即可求得.
x,根据根与系数的关系得出不等式,解不等式即可求得.
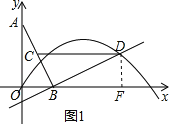
解:(1)①过点D作DF⊥x轴于点F,如图1,
∵∠DBF+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠DBF=∠BAO,
又∵∠AOB=∠BFD=90°,AB=BD,
在△AOB和△BFD中,
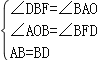 ,
,
∴△AOB≌△BFD(AAS)
∴DF=BO=1,BF=AO=2,
∴D的坐标是(3,1),
把D(3,1),E(1,1),O(0,0)代入y=ax2+bx+c,
得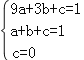 ,
,
解得a=﹣![]() ,
,
故答案为﹣![]() ;
;
(2)如图2,∵D(3,1),E(1,1),
抛物线y=ax2+bx+c过点E、D,代入可得![]() ,解得
,解得![]() ,所以y=ax2﹣4ax+3a+1.
,所以y=ax2﹣4ax+3a+1.
分两种情况:
①当抛物线y=ax2+bx+c开口向下时,若满足∠QOB与∠BCD互余且符合条件的Q点的个数是4个,则点Q在x轴的上、下方各有两个.
(i)当点Q在x轴的下方时,直线OQ与抛物线有两个交点,满足条件的Q有2个;
(ii)当点Q在x轴的上方时,要使直线OQ与抛物线y=ax2+bx+c有两个交点,抛物线y=ax2+bx+c与x轴的交点必须在x轴的正半轴上,与y轴的交点在y轴的负半轴,所以3a+1<0,解得a<﹣![]() ;
;
②当抛物线y=ax2+bx+c开口向上时,点Q在x轴的上、下方各有两个,
(i)当点Q在x轴的上方时,直线OQ与抛物线y=ax2+bx+c有两个交点,符合条件的点Q有两个;
(ii)当点Q在x轴的下方时,要使直线OQ与抛物线y=ax2+bx+c有两个交点,符合条件的点Q才两个.
根据(2)可知,要使得∠QOB与∠BCD互余,则必须∠QOB=∠BAO,
∴tan∠QOB=tan∠BAO=![]() =
=![]() ,此时直线OQ的斜率为﹣
,此时直线OQ的斜率为﹣![]() ,则直线OQ的解析式为y=﹣
,则直线OQ的解析式为y=﹣![]() x,要使直线OQ与抛物线y=ax2+bx+c有两个交点,所以方程ax2﹣4ax+3a+1=﹣
x,要使直线OQ与抛物线y=ax2+bx+c有两个交点,所以方程ax2﹣4ax+3a+1=﹣![]() x有两个不相等的实数根,所以△=(﹣4a+
x有两个不相等的实数根,所以△=(﹣4a+![]() )2﹣4a(3a+1)>0,即4a2﹣8a+
)2﹣4a(3a+1)>0,即4a2﹣8a+![]() >0,解得a>
>0,解得a>![]() (a<
(a<![]() 舍去)
舍去)
综上所示,a的取值范围为a<﹣![]() 或a>
或a>![]() .
.
故答案为a<﹣![]() 或a>
或a>![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数![]() 的图象的两个交点.
的图象的两个交点.

(1)填空:点E坐标: ;不等式![]() 的解集为 ;
的解集为 ;
(2)求正比例函数和反比例函数的关系式;
(3)P(m,n)是函数![]() 图象上的一个动点,其中0<m<3.过点P作PB⊥y轴于点B,过点A作AC⊥x轴于点C,直线PB、AC交于点D.当P为线段BD的中点时,求△POA的面积.
图象上的一个动点,其中0<m<3.过点P作PB⊥y轴于点B,过点A作AC⊥x轴于点C,直线PB、AC交于点D.当P为线段BD的中点时,求△POA的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y=![]() 图象经过点A.
图象经过点A.
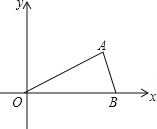
(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,试判断点D是否在该反比例函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+n.
(1)当销售单价x定为25元时,李明每月获得利润为w为1250元,则n= ;
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)当销售单价定为多少元时,每月可获得最大利润?并求最大利润为多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com