
【题目】 如图,在四边形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥CD,点E在边BC上,且∠AEB=45°,CD=10.

(1)求AB的长;
(2)求EC的长.
【答案】(1)5![]() ;(2)155
;(2)155![]() .
.
【解析】
(1)在Rt△ACD中,根据勾股定理可求AC=10![]() ,∠DAC=30°,根据平行线的性质得到∠ACB=30°,在Rt△ACB中,根据含30度角的直角三角形可求AB的长;
,∠DAC=30°,根据平行线的性质得到∠ACB=30°,在Rt△ACB中,根据含30度角的直角三角形可求AB的长;
(2)在Rt△ABE中,根据等腰直角三角形的性质可求BE,BC,再根据EC=BC-BE即可求解.
(1)在Rt△ACD中,∵∠D=60°,CD=10,
∴AD=20,
∴AC=![]() =10
=10![]() ,∠DAC=30°,
,∠DAC=30°,
又∵AD∥BC,
∵∠ACB=∠DAC=30°,
∴在Rt△ACB中,
AB=![]() AC=
AC=![]()
![]() =5
=5![]() .
.
(2)在Rt△ABE中,∠AEB=45°,
∴BE=AB=5![]() ,
,
由(1)可知,BC=![]() =15,
=15,
∴EC=BCBE=155![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,同时点
的速度移动,同时点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为
的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为![]() 秒,
秒,

![]() 求 秒后,
求 秒后, ![]() 的面积等于
的面积等于![]()
![]() 求 秒后,
求 秒后,![]() 的长度等于
的长度等于![]()
![]() 运动过程中,四边形APQC的面积能否等于
运动过程中,四边形APQC的面积能否等于![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
![]()
(1)数轴上点B表示的数是 ,点P表示的数是 ;(用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时,P、Q之间的距离恰好等于2;
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,直接写出多少秒时,P、Q之间的距离恰好等于2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=( )
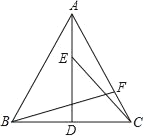
A. 112.5°B. 105°C. 90°D. 82.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮胎的直径是否符合标准,是判断轮胎质量的好与差的重要依据之一.东风轮胎厂某批轮胎的标准直径是![]() ,质量检验员从这批产品中抽取10个轮胎进行检查,超过标准直径的毫米数记为正,不足的毫米数记为负,检查记录如下(单位:
,质量检验员从这批产品中抽取10个轮胎进行检查,超过标准直径的毫米数记为正,不足的毫米数记为负,检查记录如下(单位:![]() ):
):

(1)若与标准直径比较相差不超过![]() 的为合格品,请用所学的数学知识说明第几号轮胎不合格?不合格轮胎的实际直径是多少毫米?
的为合格品,请用所学的数学知识说明第几号轮胎不合格?不合格轮胎的实际直径是多少毫米?
(2)若与标准直径比较相差不超过![]() 的为合格品,请根据抽查的结果估算一下这批轮胎的合格率大约是多少?
的为合格品,请根据抽查的结果估算一下这批轮胎的合格率大约是多少?
(3)求这10个轮胎的平均直径(精确到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:已知:如图①-1,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() ,试探究
,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)
之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)

解:(1)![]() 与
与![]() 、
、![]() 之间的数量关系是:
之间的数量关系是:![]() (或
(或![]() 只要关系式形式正确即可)
只要关系式形式正确即可)
理由:如图①-2,过点![]() 作
作![]() .
.
∵![]() (作图),
(作图),
∴![]() ( ),
( ),
∴![]() (已知)
(已知)
![]() (作图),
(作图),
∴![]() _______( ),
_______( ),
∴![]() _______( ),
_______( ),
∴![]() (等量代换)
(等量代换)
又∵![]() (角的和差),
(角的和差),
∴![]() (等量代换)
(等量代换)
总结反思:本题通过添加适当的辅助线,从而利用平行线的性质,使问题得以解决.
(2)类比探究:如图②,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() 、
、![]() ,请同学们类比(1)的解答过程,试探究
,请同学们类比(1)的解答过程,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.
之间有什么数量关系,并说明理由.
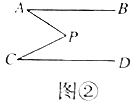
(3)拓展延伸:如图③,![]() ,
,![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数,请直接写出结果,不说明理由.
的度数,请直接写出结果,不说明理由.
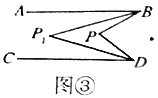
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①连接两点间的线段叫这两点的距离;
②木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;
③若![]() 三点在同一直线上,且
三点在同一直线上,且![]() ,则
,则![]() 是线段
是线段![]() 的中点;
的中点;
④若![]() ,则有
,则有![]() .
.
其中一定正确的是_________(把你认为正确结论的序号都填上) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=![]() AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.
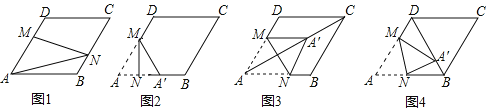
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
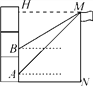
【题目】如图,小明所在教学楼的每层高度为3.5 m,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为31°,已知每层楼的窗台离该层的地面高度均为1 m.
(1)AB=________m;
(2)求旗杆MN的高度.(结果保留两位小数)
(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com