
【题目】(1)问题背景:已知:如图①-1,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() ,试探究
,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)
之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)

解:(1)![]() 与
与![]() 、
、![]() 之间的数量关系是:
之间的数量关系是:![]() (或
(或![]() 只要关系式形式正确即可)
只要关系式形式正确即可)
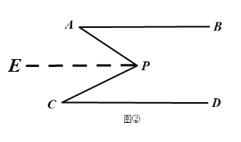
理由:如图①-2,过点![]() 作
作![]() .
.
∵![]() (作图),
(作图),
∴![]() ( ),
( ),
∴![]() (已知)
(已知)
![]() (作图),
(作图),
∴![]() _______( ),
_______( ),
∴![]() _______( ),
_______( ),
∴![]() (等量代换)
(等量代换)
又∵![]() (角的和差),
(角的和差),
∴![]() (等量代换)
(等量代换)
总结反思:本题通过添加适当的辅助线,从而利用平行线的性质,使问题得以解决.
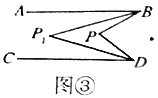
(2)类比探究:如图②,![]() ,点
,点![]() 的位置如图所示,连结
的位置如图所示,连结![]() 、
、![]() ,请同学们类比(1)的解答过程,试探究
,请同学们类比(1)的解答过程,试探究![]() 与
与![]() 、
、![]() 之间有什么数量关系,并说明理由.
之间有什么数量关系,并说明理由.
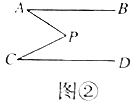
(3)拓展延伸:如图③,![]() ,
,![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数,请直接写出结果,不说明理由.
的度数,请直接写出结果,不说明理由.
【答案】(1)∠APC+∠PAB+∠PCD=360°,理由见解析;两直线平行,同旁内角互补;CD,如果两条直线都和第三条直线平行,那么这两条直线也互相平行;180°,两直线平行,同旁内角互补;(2)∠APC=∠PAB+∠PCD,理由见解析;(3)∠P=56°.
【解析】
(1)如图②,过点P作PE∥AB,依据平行线的性质,即可得到![]() 与
与![]() 、
、![]() 之间的数量关系;
之间的数量关系;
(2)过点P作PE∥AB,依据平行线的性质,即可得出∠APE=∠PAB,∠CPE=∠PCD,进而得到∠APC=∠APE+∠CPE,即可得到∠APC=∠PAB+∠PCD;
(3)根据角平分线的性质及平行线的性质求解即可.
(1)∠APC与∠PAB、∠PCD之间的关系是:∠APC+∠PAB+∠PCD=360°
(或∠APC=360°-(∠PAB+∠PCD)只要关系式形式正确即可)
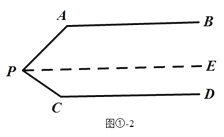
理由:如图①-2,过点P作PE∥AB.
∵PE∥AB(作图),
∴∠PAB+∠APE=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
PE∥AB(作图),
∴PE∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠CPE+∠PCD=180°(两直线平行,同旁内角互补),
∴∠PAB+∠APE+∠CPE+∠PCD=180°+180°=360°(等量代换)
又∵∠APE+∠CPE=∠APC(角的和差),
∴∠APC+∠PAB+∠PCD=360°(等量代换)
(2)∠APC与∠PAB、∠PCD之间的关系是:∠APC=∠PAB+∠PCD
理由:过点P作PE∥AB,
∴∠PAB=∠APE(两直线平行,内错角相等)
∵AB∥CD(已知)
PE∥AB(作图),
∴PE∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠PCD=∠CPE(两直线平行,内错角相等)
∵∠APE+∠CPE=∠APC(角的和差),
∴∠APC=∠PAB+∠PCD(等量代换)
(3)∠P=56°.

理由:如图③,∵![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,
∴∠PBA=2∠![]() BA, ∠PDC=2∠
BA, ∠PDC=2∠![]() DC,
DC,
∴∠PBA+ ∠PDC=2(∠![]() BA+
BA+![]() DC)
DC)
由(2)可得: ∠P=∠PBA+∠PDC, ∠![]() =∠AB
=∠AB![]() +∠CD
+∠CD![]()
∴∠P=2(∠![]() BA+
BA+![]() DC)=2∠
DC)=2∠![]() =2×28°=56°
=2×28°=56°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连接CD.若AB=4cm.则△BCD的面积为( )

A. 4![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:其中正确的个数是()
(1)有一个角为60°的等腰三角形是等边三角形;
(2)三角之比为3:4:5的三角形为直角三角形;
(3)等腰三角形的两条边长为2,4,则等腰三角形的周长为10;
(4)一边上的中线等于这边长的一半的三角形是等边三角形;
A.2个B.3个C.4个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在四边形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥CD,点E在边BC上,且∠AEB=45°,CD=10.

(1)求AB的长;
(2)求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c (a,b,c为常数,且a≠0)经过点(﹣1,0)、(m,0),且1<m<2,当x<﹣1时,y随x增大而减小,下列结论:①abc>0;②a+b<0;③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;④a(m﹣1)+b=0;⑤c≤﹣1时,则b2﹣4ac≤4a.其中结论正确的有( )个
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
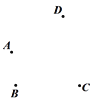
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盐城市某校开展了向贫困山区捐赠图书活动.全校2000名学生每人都捐赠了一定数量的图书,已知各年级人数分布的扇形统计图如图①所示.学校为了了解各年级捐赠图书情况,从各年级中随机抽查了部分学年生,进行捐赠图书情况的统计,绘制成如图②的频数分布直方图.根据以上信息解答下列问题:
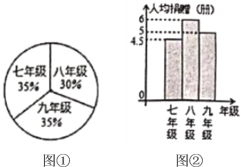
(1)人均捐赠图书最多的是 年级;
(2)估计该校九年级学生共捐赠图书多少册?
(3)全校大约共捐赠图书多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施. 如图所示,京张高铁起自北京北站,途经清河、沙河、吕平等站,终点站为张家口南站,全长174千米.
(1)根据资料显示,京张高铁的客运价格拟定为0. 4元(人·千米),可估计京张高铁单程票价约为_________元(结果精确到个位);
(2)京张高铁建成后,将是世界上第一条设计时速为350千米/时的高速铁路. 乘高铁从北京到张家口的时间将缩短至1小时,如果按此设计时速运行,那么每站(不计起始站和终点站)停靠的平均时间是多少分钟?(结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com