
ΓΨΧβΡΩΓΩ―Έ≥« –Ρ≥–ΘΩΣ’ΙΝΥœρΤΕάß…Ϋ«χΨη‘υΆΦ ιΜνΕ·Θ°»Ϊ–Θ2000Οϊ―ß…ζΟΩ»ΥΕΦΨη‘υΝΥ“ΜΕ® ΐΝΩΒΡΆΦ ιΘ§“―÷ΣΗςΡξΦΕ»Υ ΐΖ÷≤ΦΒΡ…»–ΈΆ≥ΦΤΆΦ»γΆΦΔΌΥυ ΨΘ°―ß–ΘΈΣΝΥΝΥΫβΗςΡξΦΕΨη‘υΆΦ ι«ιΩωΘ§¥”ΗςΡξΦΕ÷–ΥφΜζ≥ι≤ιΝΥ≤ΩΖ÷―ßΡξ…ζΘ§Ϋχ––Ψη‘υΆΦ ι«ιΩωΒΡΆ≥ΦΤΘ§Μφ÷Τ≥…»γΆΦΔΎΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ°ΗυΨί“‘…œ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
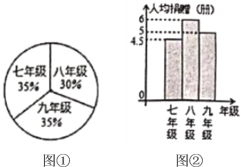
Θ®1Θ©»ΥΨυΨη‘υΆΦ ιΉνΕύΒΡ « ΡξΦΕΘΜ
Θ®2Θ©ΙάΦΤΗΟ–ΘΨ≈ΡξΦΕ―ß…ζΙ≤Ψη‘υΆΦ ιΕύ…Ό≤αΘΩ
Θ®3Θ©»Ϊ–Θ¥σ‘ΦΙ≤Ψη‘υΆΦ ιΕύ…Ό≤αΘΩ
ΓΨ¥πΑΗΓΩΫβΘΚΘ®1Θ©ΑΥΘΜΘ®2Θ©700»ΥΘ§3500≤αΘΜΘ®2Θ©16600≤αΘΜ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧθ–ΈΆ≥ΦΤΆΦΦ¥Ω…≈–Εœ»ΥΨυΨη‘υΆΦ ιΉνΕύΒΡ «ΑΥΡξΦΕΘΜ
Θ®2Θ©œ»«σ≥ωΨ≈ΡξΦΕΒΡ»Υ ΐΘ§‘ΌΗυΨί»ΥΨυΨη‘υΆΦ ιΦ¥Ω…«σΫβΘΜ
Θ®3Θ©œ»Υψ≥ωΗςΡξΦΕΒΡΨη ι ΐΝΩΘ§œύΦ”.
Θ®1Θ©»ΥΨυΨη‘υΆΦ ιΉνΕύΒΡ «ΑΥΡξΦΕΘΜ
Ι ¥πΑΗΈΣΘΚΑΥΘΜ
Θ®2Θ©Ψ≈ΡξΦΕΒΡ―ß…ζ»Υ ΐΈΣ2000ΓΝ35%ΘΫ700Θ®»ΥΘ©Θ§
ΙάΦΤΨ≈ΡξΦΕΙ≤Ψη‘υΆΦ ιΈΣ700ΓΝ5ΘΫ3500Θ®≤αΘ©Θ°
Θ®3Θ©2000ΓΝ35%ΓΝ4.5ΘΪ2000ΓΝ35%ΓΝ5ΘΪ2000ΓΝ30%ΓΝ6ΘΫ10250Θ®≤αΘ©Θ°
¥πΘΚΙάΦΤ»Ϊ–ΘΙ≤Ψη‘υΆΦ ι10250≤αΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–ΈΆχ¬γ÷–Θ§ΓςABCΒΡ»ΐΗωΕΞΒψΕΦ‘ΎΗώΒψ…œΘ§ΒψAΓΔBΓΔCΒΡΉχ±ξΖ÷±πΈΣA(-2Θ§4)ΓΔB(-2Θ§0)ΓΔC(-4Θ§1)Θ§ΫαΚœΥυΗχΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒΫβ¥πœ¬Ν–Έ ΧβΘΚ
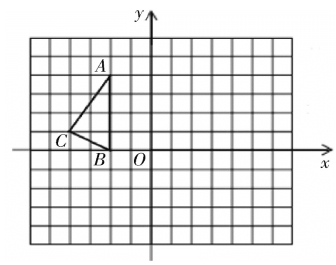
Θ®1Θ©Μ≠≥ωΓςABCΙΊ”Ύ‘≠ΒψO÷––ΡΕ‘≥ΤΆΦ–ΈΓςA1B1C1.
Θ®2Θ©ΤΫ“ΤΓςABCΘ§ ΙΒψA“ΤΕ·ΒΫΒψA2(0Θ§2)Θ§Μ≠≥ωΤΫ“ΤΚσΒΡΓςA2B2C2≤Δ–¥≥ωΒψB2ΓΔC2ΒΡΉχ±ξ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©Έ Χβ±≥ΨΑΘΚ“―÷ΣΘΚ»γΆΦΔΌ-1Θ§![]() Θ§Βψ
Θ§Βψ![]() ΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§Ν§Ϋα
ΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§Ν§Ϋα![]() Θ§ ‘ΧΫΨΩ
Θ§ ‘ΧΫΨΩ![]() ”κ
”κ![]() ΓΔ
ΓΔ![]() ÷°Φδ”– ≤Ο¥ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°(ΫΪœ¬ΟφΒΡΫβ¥πΙΐ≥Χ≤Ι≥δΆξ’ϊΘ§ά®Κ≈ΡΎ–¥…œœύ”Πάμ”…Μρ ΐ―ß Ϋ)
÷°Φδ”– ≤Ο¥ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°(ΫΪœ¬ΟφΒΡΫβ¥πΙΐ≥Χ≤Ι≥δΆξ’ϊΘ§ά®Κ≈ΡΎ–¥…œœύ”Πάμ”…Μρ ΐ―ß Ϋ)

ΫβΘΚΘ®1Θ©![]() ”κ
”κ![]() ΓΔ
ΓΔ![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒ «ΘΚ
÷°ΦδΒΡ ΐΝΩΙΊœΒ «ΘΚ![]() (Μρ
(Μρ![]() ÷Μ“ΣΙΊœΒ Ϋ–Έ Ϋ’ΐ»ΖΦ¥Ω…)
÷Μ“ΣΙΊœΒ Ϋ–Έ Ϋ’ΐ»ΖΦ¥Ω…)
άμ”…ΘΚ»γΆΦΔΌ-2Θ§ΙΐΒψ![]() Ής
Ής![]() Θ°
Θ°
ΓΏ![]() (ΉςΆΦ)Θ§
(ΉςΆΦ)Θ§
Γύ![]() (ΓΓΓΓ)Θ§
(ΓΓΓΓ)Θ§
Γύ![]() (“―÷Σ)
(“―÷Σ)
![]() (ΉςΆΦ)Θ§
(ΉςΆΦ)Θ§
Γύ![]() _______(ΓΓΓΓ)Θ§
_______(ΓΓΓΓ)Θ§
Γύ![]() _______(ΓΓΓΓ)Θ§
_______(ΓΓΓΓ)Θ§
Γύ![]() (Β»ΝΩ¥ζΜΜ)
(Β»ΝΩ¥ζΜΜ)
”÷ΓΏ![]() (Ϋ«ΒΡΚΆ≤ν)Θ§
(Ϋ«ΒΡΚΆ≤ν)Θ§
Γύ![]() (Β»ΝΩ¥ζΜΜ)
(Β»ΝΩ¥ζΜΜ)
ΉήΫαΖ¥ΥΦΘΚ±ΨΧβΆ®ΙΐΧμΦ” Β±ΒΡΗ®÷ζœΏΘ§¥”Εχάϊ”ΟΤΫ––œΏΒΡ–‘÷ Θ§ ΙΈ ΧβΒΟ“‘ΫβΨωΘ°
Θ®2Θ©άύ±»ΧΫΨΩΘΚ»γΆΦΔΎΘ§![]() Θ§Βψ
Θ§Βψ![]() ΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§Ν§Ϋα
ΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§Ν§Ϋα![]() ΓΔ
ΓΔ![]() Θ§«κΆ§―ßΟ«άύ±»Θ®1Θ©ΒΡΫβ¥πΙΐ≥ΧΘ§ ‘ΧΫΨΩ
Θ§«κΆ§―ßΟ«άύ±»Θ®1Θ©ΒΡΫβ¥πΙΐ≥ΧΘ§ ‘ΧΫΨΩ![]() ”κ
”κ![]() ΓΔ
ΓΔ![]() ÷°Φδ”– ≤Ο¥ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
÷°Φδ”– ≤Ο¥ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
Θ®3Θ©ΆΊ’Ι―”…λΘΚ»γΆΦΔέΘ§![]() Θ§
Θ§![]() ”κ
”κ![]() ΒΡΤΫΖ÷œΏœύΫΜ”ΎΒψ
ΒΡΤΫΖ÷œΏœύΫΜ”ΎΒψ![]() Θ§»τ
Θ§»τ![]() Θ§«σ
Θ§«σ![]() ΒΡΕ» ΐΘ§«κ÷±Ϋ”–¥≥ωΫαΙϊΘ§≤ΜΥΒΟςάμ”…Θ°
ΒΡΕ» ΐΘ§«κ÷±Ϋ”–¥≥ωΫαΙϊΘ§≤ΜΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
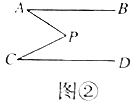
ΓΨΧβΡΩΓΩΘ®–¬Ε®“εΘ©ΘΚAΓΔBΓΔC ΈΣ ΐ÷α…œ»ΐΒψΘ§»τΒψ C ΒΫ A ΒΡΨύάκ «Βψ C ΒΫ B ΒΡΨύάκΒΡ 3 ±ΕΘ§Έ“Ο«ΨΆ≥ΤΒψ
C «Θ®AΘ§BΘ©ΒΡ–“‘ΥΒψΘ°
Θ®ΧΊάΐΗ–÷ΣΘ©ΘΚ
Θ®1Θ©»γΆΦ 1Θ§Βψ A ±μ ΨΒΡ ΐΈΣ©¹1Θ§Βψ B ±μ ΨΒΡ ΐΈΣ 3Θ°±μ Ψ 2 ΒΡΒψ C ΒΫΒψ A ΒΡΨύάκ « 3Θ§ ΒΫΒψ B ΒΡΨύάκ « 1Θ§Ρ«Ο¥Βψ C «Θ®AΘ§BΘ©ΒΡ–“‘ΥΒψΘ°
ΔΌΘ®BΘ§AΘ©ΒΡ–“‘ΥΒψ±μ ΨΒΡ ΐ « ΘΜAΘ°©¹1ΘΜ B.0ΘΜ C.1ΘΜ D.2
ΔΎ ‘ΥΒΟς A «Θ®CΘ§EΘ©ΒΡ–“‘ΥΒψΘ°
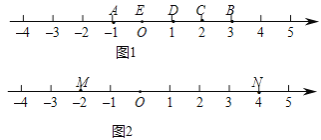
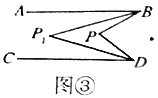
Θ®2Θ©»γΆΦ 2Θ§MΓΔN ΈΣ ΐ÷α…œΝΫΒψΘ§Βψ M Υυ±μ ΨΒΡ ΐΈΣ©¹2Θ§Βψ N Υυ±μ ΨΒΡ ΐΈΣ 4Θ§‘ρΘ®MΘ§NΘ©ΒΡ–“Βψ ΨΒΡ ΐΈΣ Θ°
Θ®ΆΊ’Ι”Π”ΟΘ©ΘΚ
Θ®3Θ©»γΆΦ 3Θ§AΓΔB ΈΣ ΐ÷α…œΝΫΒψΘ§Βψ A Υυ±μ ΨΒΡ ΐΈΣ©¹20Θ§Βψ B Υυ±μ ΨΒΡ ΐΈΣ 40Θ°œ÷”–“Μ÷ΜΒγΉ”¬λ“œ P ¥”Βψ B ≥ωΖΔΘ§“‘ 3 ΗωΒΞΈΜΟΩΟκΒΡΥΌΕ»œρΉσ‘ΥΕ·Θ§ΒΫ¥οΒψ A ΆΘ÷ΙΘ°Β± t ΈΣΚΈ÷Β ±Θ§PΓΔA ΚΆ B »ΐΗωΒψ÷–«ΓΚΟ”–“ΜΗωΒψΈΣΤδ”ύΝΫΒψΒΡ–“‘ΥΒψΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΆΦ1©¹©¹ΆΦ4÷–Θ§Νβ–ΈABCDΒΡ±Ώ≥ΛΈΣ3Θ§ΓœA=60ΓψΘ§ΒψM «AD±Ώ…œ“ΜΒψΘ§«“DM=![]() ADΘ§ΒψN «’έœΏAB©¹BC…œΒΡ“ΜΗωΕ·ΒψΘ°
ADΘ§ΒψN «’έœΏAB©¹BC…œΒΡ“ΜΗωΕ·ΒψΘ°
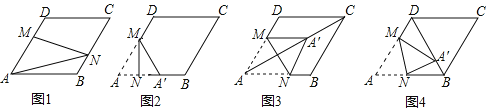
Θ®1Θ©»γΆΦ1Θ§Β±N‘ΎBC±Ώ…œΘ§«“MNΙΐΕ‘Ϋ«œΏAC”κBDΒΡΫΜΒψ ±Θ§‘ρœΏΕΈANΒΡ≥ΛΕ»ΈΣ Θ°
Θ®2Θ©Β±ΒψN‘ΎAB±Ώ…œ ±Θ§ΫΪΓςAMN―ΊMNΖ≠’έΒΟΒΫΓςAΓδMNΘ§»γΆΦ2Θ§
ΔΌ»τΒψAΓδ¬δ‘ΎAB±Ώ…œΘ§‘ρœΏΕΈANΒΡ≥ΛΕ»ΈΣ ΘΜ
ΔΎΒ±ΒψAΓδ¬δ‘ΎΕ‘Ϋ«œΏAC…œ ±Θ§»γΆΦ3Θ§«σ÷ΛΘΚΥΡ±Ώ–ΈAM AΓδN «Νβ–ΈΘΜ
ΔέΒ±ΒψAΓδ¬δ‘ΎΕ‘Ϋ«œΏBD…œ ±Θ§»γΆΦ4Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2017Ρξ»Ϊ«ρ≥§ΦΕΦΤΥψΜζ500«ΩΟϊΒΞΙΪ≤ΦΘ§÷–Ιζ≥§ΦΕΦΤΥψΜζΓΑ…ώΆΰΓΛΧΪΚΰ÷°ΙβΓ±ΚΆΓΑΧλΚ”ΕΰΚ≈Γ±–· ÷ΕαΒΟ«ΑΝΫΟϊΘ°“―÷ΣΓΑ…ώΆΰΓΛΧΪΚΰ÷°ΙβΓ±ΒΡΗΓΒψ‘ΥΥψΥΌΕ» «ΓΑΧλΚ”ΕΰΚ≈Γ±ΒΡ2.74±ΕΘ°’βΝΫ÷÷≥§ΦΕΦΤΥψΜζΖ÷±πΫχ––100“Ύ“Ύ¥ΈΗΓΒψ‘ΥΥψΘ§ΓΑ…ώΆΰΓΛΧΪΚΰ÷°ΙβΓ±ΒΡ‘ΥΥψ ±Φδ±»ΓΑΧλΚ”ΕΰΚ≈Γ±…Ό18.75ΟκΘ§«σ’βΝΫ÷÷≥§ΦΕΦΤΥψΜζΒΡΗΓΒψ‘ΥΥψΥΌΕ»Θ°…ηΓΑΧλΚ”ΕΰΚ≈Γ±ΒΡΗΓΒψ‘ΥΥψΥΌΕ»ΈΣ![]() “Ύ“Ύ¥Έ/ΟκΘ§“άΧβ“βΘ§Ω…Ν–ΖΫ≥ΧΈΣ___________Θ°
“Ύ“Ύ¥Έ/ΟκΘ§“άΧβ“βΘ§Ω…Ν–ΖΫ≥ΧΈΣ___________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈABC÷–Θ§![]() Θ§
Θ§![]() Θ§D «ABΒΡ÷–ΒψΘ§EΓΔFΖ÷±π «ACΓΔBC…œΒΡΒψΘ®ΒψE≤Μ”κΕΥΒψAΓΔC÷ΊΚœΘ©Θ§Ν§Ϋ”EF≤Δ»ΓEFΒΡ÷–ΒψOΘ§Ν§Ϋ”DO≤Δ―”≥Λ÷ΝΒψGΘ§ Ι
Θ§D «ABΒΡ÷–ΒψΘ§EΓΔFΖ÷±π «ACΓΔBC…œΒΡΒψΘ®ΒψE≤Μ”κΕΥΒψAΓΔC÷ΊΚœΘ©Θ§Ν§Ϋ”EF≤Δ»ΓEFΒΡ÷–ΒψOΘ§Ν§Ϋ”DO≤Δ―”≥Λ÷ΝΒψGΘ§ Ι![]() Θ§Ν§Ϋ”DEΓΔGEΓΔGF.
Θ§Ν§Ϋ”DEΓΔGEΓΔGF.
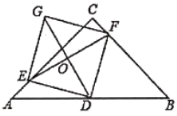
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈEDFG «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©»τ![]() Θ§ΧΫΨΩΥΡ±Ώ–ΈEDFGΒΡ–ΈΉ¥ΘΩ
Θ§ΧΫΨΩΥΡ±Ώ–ΈEDFGΒΡ–ΈΉ¥ΘΩ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Β±EΒψ‘ΎΚΈ¥Π ±Θ§ΥΡ±Ώ–ΈEDFGΒΡΟφΜΐΉν–ΓΘ§≤Δ«σ≥ωΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
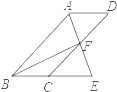
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCDΈΣΤΫ––ΥΡ±Ώ–ΈΘ§ΓœBADΒΡΫ«ΤΫΖ÷œΏAEΫΜCD”ΎΒψFΘ§ΫΜBCΒΡ―”≥ΛœΏ”ΎΒψEΘ°
Θ®1Θ©«σ÷ΛΘΚBE=CDΘΜ
Θ®2Θ©Ν§Ϋ”BFΘ§»τBFΓΆAEΘ§ΓœBEA=60ΓψΘ§AB=4Θ§«σΤΫ––ΥΡ±Ώ–ΈABCDΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥―ß–ΘΦΤΜ°ΙΚΫχAΘ§BΝΫ÷÷ ςΡΨΙ≤100ΩΟΫχ–––Θ‘Α¬ΧΜ·…ΐΦΕΘ§Ψ≠ –≥ΓΒς≤ιΘΚΙΚ¬ρA÷÷ ςΡΨ2ΩΟΘ§B÷÷ ςΡΨ5ΩΟΘ§Ι≤–η600‘ΣΘΜΙΚ¬ρA÷÷ ςΡΨ3ΩΟΘ§B÷÷ ςΡΨ1ΩΟΘ§Ι≤–η380‘ΣΘ°
Θ®1Θ©«σA÷÷Θ§B÷÷ ςΡΨΟΩΩΟΗςΕύ…Ό‘ΣΘΩ
Θ®2Θ©“ρ≤ΦΨ÷–η“ΣΘ§ΙΚ¬ρA÷÷ ςΡΨΒΡ ΐΝΩ≤Μ…Ό”ΎB÷÷ ςΡΨ ΐΝΩΒΡ3±ΕΘ°―ß–Θ”κ÷–±ξΙΪΥΨ«©Ε©ΒΡΚœΆ§÷–ΙφΕ®ΘΚ‘Ύ –≥ΓΦέΗώ≤Μ±δΒΡ«ιΩωœ¬Θ®≤ΜΩΦ¬«ΤδΥϊ“ρΥΊΘ©Θ§ ΒΦ ΗΕΩνΉήΫπΕνΑ¥ –≥ΓΦέΨ≈’έ”≈ΜίΘ§«κ…ηΦΤ“Μ÷÷ΙΚ¬ρ ςΡΨΒΡΖΫΑΗΘ§ Ι ΒΦ ΥυΜ®Ζ―”ΟΉν ΓΘ§≤Δ«σ≥ωΉν ΓΒΡΖ―”ΟΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com