
【题目】如图,在等腰直角三角形ABC中,![]() ,
,![]() ,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使
,D是AB的中点,E、F分别是AC、BC上的点(点E不与端点A、C重合),连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE、GE、GF.
,连接DE、GE、GF.
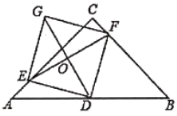
(1)求证:四边形EDFG是平行四边形;
(2)若![]() ,探究四边形EDFG的形状?
,探究四边形EDFG的形状?
(3)在(2)的条件下,当E点在何处时,四边形EDFG的面积最小,并求出最小值.
【答案】(1)详见解析;(2)详见解析;(3)当E点在AC中点时,四边形EDGF的面积最小为4.
【解析】
(1)根据对角线互相平分的四边形是平行四边形可得结论;
(2)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据(1)中的结论,由此即可证出四边形EDFG是正方形;
(3)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2![]() ,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
(1)证明:∵O是EF的中点,
∴OE=OF,
∵OG=OD,
∴四边形EDFG是平行四边形;
(2)解:四边形EDFG是正方形,理由是:
连接CD,如图1所示,
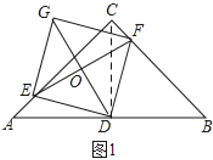
∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,
∴∠A=∠DCF=45°,AD=CD.
在△ADE和△CDF中,
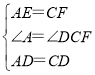 ,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
由(1)知:四边形EDFG是平行四边形;
∴四边形EDFG是正方形;
(3)解:过点D作DE′⊥AC于E′,如图2所示.
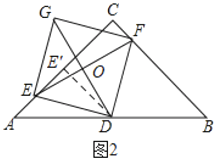
∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,
∴DE′=![]() BC=2,AB=4
BC=2,AB=4![]() ,点E′为AC的中点,
,点E′为AC的中点,
∴2≤DE<2![]() (点E与点E′重合时取等号).
(点E与点E′重合时取等号).
∴4≤S四边形EDFG=DE2<8.
∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.


科目:初中数学 来源: 题型:
【题目】有下列说法:其中正确的个数是()
(1)有一个角为60°的等腰三角形是等边三角形;
(2)三角之比为3:4:5的三角形为直角三角形;
(3)等腰三角形的两条边长为2,4,则等腰三角形的周长为10;
(4)一边上的中线等于这边长的一半的三角形是等边三角形;
A.2个B.3个C.4个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盐城市某校开展了向贫困山区捐赠图书活动.全校2000名学生每人都捐赠了一定数量的图书,已知各年级人数分布的扇形统计图如图①所示.学校为了了解各年级捐赠图书情况,从各年级中随机抽查了部分学年生,进行捐赠图书情况的统计,绘制成如图②的频数分布直方图.根据以上信息解答下列问题:
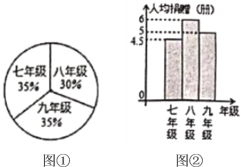
(1)人均捐赠图书最多的是 年级;
(2)估计该校九年级学生共捐赠图书多少册?
(3)全校大约共捐赠图书多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
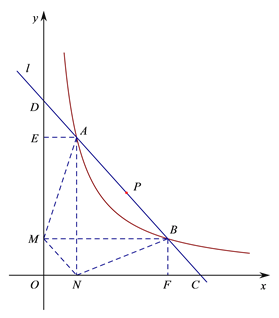
【题目】已知直线![]() 过点
过点![]() ,且与函数
,且与函数![]() 的图象相交于
的图象相交于![]() 两点,与
两点,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,如图所示,四边形
,如图所示,四边形![]() 均为矩形,且矩形
均为矩形,且矩形![]() 的面积为
的面积为![]() .
.
(1)求![]() 的值;
的值;
(2)当点![]() 的横坐标为
的横坐标为![]() 时,求直线
时,求直线![]() 的解析式及线段
的解析式及线段![]() 的长;
的长;
(3)如图是小芳同学对线段![]() 的长度关系的思考示意图.记点
的长度关系的思考示意图.记点![]() 的横坐标为
的横坐标为![]() ,已知当
,已知当![]() 时,线段
时,线段![]() 的长随
的长随![]() 的增大而减小,请你参考小芳的示意图判断:当
的增大而减小,请你参考小芳的示意图判断:当![]() 时,线段
时,线段![]() 的长随
的长随![]() 的增大而 . (填“增大”、“减小”或“不变”)
的增大而 . (填“增大”、“减小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①OG=![]() AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.其中正确的是( )
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.其中正确的是( )
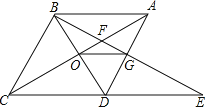
A.①④B.①③④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施. 如图所示,京张高铁起自北京北站,途经清河、沙河、吕平等站,终点站为张家口南站,全长174千米.
(1)根据资料显示,京张高铁的客运价格拟定为0. 4元(人·千米),可估计京张高铁单程票价约为_________元(结果精确到个位);
(2)京张高铁建成后,将是世界上第一条设计时速为350千米/时的高速铁路. 乘高铁从北京到张家口的时间将缩短至1小时,如果按此设计时速运行,那么每站(不计起始站和终点站)停靠的平均时间是多少分钟?(结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com