
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.

【答案】(1)证明见解析;(2)S△ADG=1+![]() .
.
【解析】
(1)利用正方形得到条件,判断出△ADG≌△ABE,根据全等三角形的性质即可得到结论;
(2)利用正方形的性质在Rt△AMD中,∠MDA=45°,AD=2从而得出AM=DM=![]() ,在Rt△AMG中,AM2+GM2=AG2从而得出GM=
,在Rt△AMG中,AM2+GM2=AG2从而得出GM=![]() 即可.
即可.
(1)解:如图1,延长EB交DG于点H,
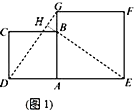
∵四边形ABCD与四边形AEFG是正方形,
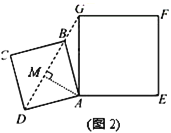
∴AD=AB,∠DAG=∠BAE=90°,AG=AE
在△ADG与△ABE中,
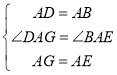
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,
∵△ADG中∠AGD+∠ADG=90°,
∴∠AEB+∠ADG=90°,
∵△DEH中,∠AEB+∠ADG+∠DHE=180°,
∴∠DHE=90°,
∴DG⊥BE.
(2)解:如图2,过点A作AM⊥DG交DG于点M,
∠AMD=∠AMG=90°,
∵BD是正方形ABCD的对角,
∴∠MDA=45°
在Rt△AMD中,∵∠MDA=45°,AD=2,
∴AM=DM=![]() ,
,
在Rt△AMG中,
∵AM2+GM2=AG2,
∴GM=![]() ,
,
∵DG=DM+GM=![]() ,
,
∴S△ADG=![]() =1+
=1+![]() .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当矩形ABCD的长和宽满足什么条件时,四边形MENF是正方形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边BC在x轴上,且∠ACB=90°.反比例函数y=![]() (x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
(x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
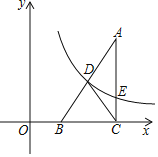
(1)求k的值;(2)若AE=BC,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
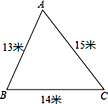
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
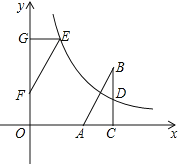
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:

①菜地离小明家多远?小明走到菜地用了多少时间?
②小明给菜地浇水用了多少时间?
③玉米地离菜地、小明家多远?小明从玉米地走回家平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?
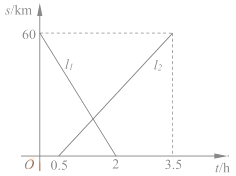
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列横线上用含有![]() ,
,![]() 的代数式表示相应图形的面积.
的代数式表示相应图形的面积.
(1)①________;②__________;③__________;④_________________.
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:________________________________________.
(3)利用(2)的结论计算1972+2×197×3+32的值.( 注意不利用以上结论不得分)
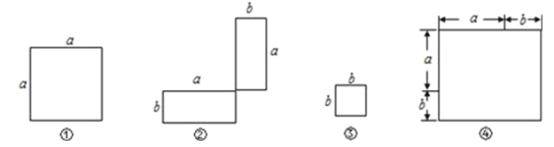
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(![]() ,0),B(
,0),B(![]() ,0),C(0,2)三点.
,0),C(0,2)三点.
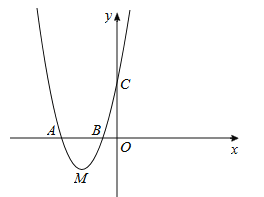
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com