
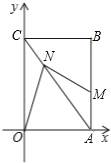
【题目】已知:矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正半轴上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点到达终点时,另一点即停止运动.设运动的时间为t秒.
(1)当点N运动1秒时,求点N的坐标;(提示:过N作x轴y轴垂线,垂足分别为D,ECN:CA=CE:CO=NE:OA)
(2)试求出多边形OAMN的面积S与t的函数关系式;
(3)t为何值时,以△OAN的一边所在直线为对称轴翻折△OAN,翻折前后的两个三角形所组成的四边形为菱形?
【答案】(1)N的坐标为![]() ;
;
(2)多边形OAMN的面积S=![]() ,(0≤t≤4).
,(0≤t≤4).
(3)t的值为![]() ,
,![]() 或
或![]() .
.
【解析】试题分析:(1)过N作NE⊥y轴,作NF⊥x轴,由△CEN∽△COA,利用相似比求EN,再用勾股定理求CE,确定N点坐标;(2)将多边形OAMN分为△ONA和△AMN,用t分别表示两个三角形的面积,再求和即可;(3)分为①直线ON为对称轴,②直线OA为对称轴,③直线AN为对称轴,画出图形,根据菱形的特殊性,列方程求解.
试题解析:(1)∵t=1∴CN=1,AM=1
过N作NE⊥y轴,作NF⊥x轴
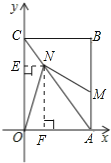
过N作NE⊥y轴,NF⊥x轴,
∴△CEN∽△COA,
∴![]() ,即
,即![]() ,
,
∴EN=![]() .
.
由勾股定理得:![]() ,
,![]() ,
,
∴![]() .
.
(2)由(1)得![]() ,∴
,∴![]() ,
,
∴N点坐标为![]() .
.
∵多边形OAMN由△ONA和△AMN组成
∴![]() ,
,![]() ,
,
∴多边形OAMN的面积S=![]() (0≤t≤4).
(0≤t≤4).
(3)①直线ON为对称轴时,翻折△OAN得到△OA′N,此时组成的四边形为OANA′,
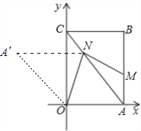
当AN=A′N=A′O=OA,四边形OANA’是菱形.
即AN=OA,∴5-t=3∴t=2.
②直线OA为对称轴时,翻折△OAN得到△OAN′,
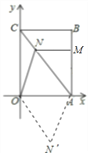
此时组成的四边形为ONAN′,连接NN′,交OA于点G.
当NN′与OA互相垂直平分时,四边形ONAN′是菱形.
即OA⊥NN′,OG=AG=![]() ,
,
∴NG∥CO,∴点N是AC的中点,
∴CN=![]() ,∴
,∴![]()
③直线AN为对称轴时,翻折△OAN得到△O′AN,
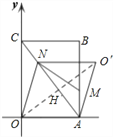
此时组成的四边形为ONO′A,连接OO’,交AN于点H.
当OO′与AN互相垂直平分时,四边形ONO’A是菱形.
即OH⊥AC,AH=NH=![]() ,
,
由面积法可求得OH=![]() ,
,
在Rt△OAH中,由勾股定理得,AH=![]() .
.
∴![]() ,∴
,∴![]()
综上所述,t的值为![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
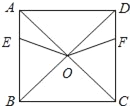
【题目】已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.
(1)求证:OE=OF.
(2)在点E、F的运动过程中,连结AF.设线段AE、OE、OF、AF所形成的图形面积为S.
探究:①S的大小是否会随着运动时间为t的变化而变化?若会变化,试求出S与t的函数关系式;若不会变化,请说明理由.
②连结EF,当运动时间为t为何值时,△OEF的面积恰好等于的![]() S.
S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲厂有某种原料180吨,运出2x吨,乙厂有同样的原料120吨,运进x吨,现在甲厂原料比乙厂原料多30吨,根据题意列方程,则下列所列方程正确的是( )
A.(180﹣2x)﹣(120+x)=30
B.(180+2x)﹣(120﹣x)=30
C.(180﹣2x)﹣(120﹣x)=30
D.(180+2x)﹣(120+x)=30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC和ΔDEF中,AB=DE,∠A=∠D,若证ΔABC≌ΔDEF还要从下列条件中补选一个,错误的选法是( )
A.∠B=∠EB.∠C=∠FC.AC=DFD.BC=EF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com