
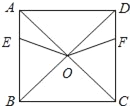
【题目】已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.
(1)求证:OE=OF.
(2)在点E、F的运动过程中,连结AF.设线段AE、OE、OF、AF所形成的图形面积为S.
探究:①S的大小是否会随着运动时间为t的变化而变化?若会变化,试求出S与t的函数关系式;若不会变化,请说明理由.
②连结EF,当运动时间为t为何值时,△OEF的面积恰好等于的![]() S.
S.
【答案】(1)见解析(2)①见解析②t为时
【解析】试题分析:(1)根据正方形的性质得出OA=OD,∠EAO=∠FDO=45°,求出AE=DF=t,根据SAS推出△EAO≌△FDO即可;
(2)①延长EO交DC于M,求出△AOE≌△COM,根据全等三角形的性质得出AE=CM=t,根据S=S四边形AEMF﹣S△FOM求出即可;
②根据全等得出OE=OM,求出S△EOF=S△EFM=16﹣4t,即可得出方程16﹣4t=×16,求出即可.
(1)证明:∵四边形ABCD是正方形,
∴OA=OD,∠EAO=∠FDO=45°,
∵点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t,
∴AE=DF=t,
在△EAO和△FDO中
![]()
∴△EAO≌△FDO(SAS),
∴OE=OF;
(2)解:①S的大小不会随着运动时间为t的变化而变化,

理由是:延长EO交DC于M,
∵四边形ABCD是正方形,
∴∠OAE=∠MCO=45°,OA=OC,
在△AOE和△COM中
![]()
∴△AOE≌△COM(ASA),
∴AE=CM=t,
∴S=S四边形AEMF﹣S△FOM
=(t+8﹣t﹣t)8﹣×(8﹣t﹣t)4
=16,
所以S的大小不会随着运动时间为t的变化而变化;
②∵△AOE≌△COM,
∴OE=OM,
∴S△EOF=S△FOM=S△EFM=×(8﹣t﹣t)8=16﹣4t,
∵△OEF的面积恰好等于的S,
∴16﹣4t=×16,
解得:t=,
即当运动时间为t为时,△OEF的面积恰好等于的S.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
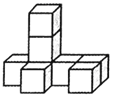
【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
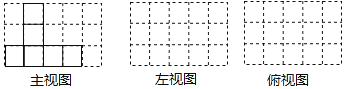
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下面的网格中画出添加小正方体后所得几何体所有可能的左视图.
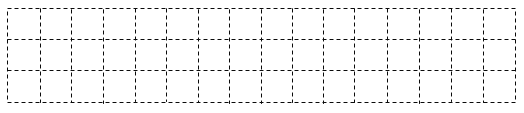
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温家宝总理有句名言:“多么小的问题乘以13亿,都会变得很大;多么大的经济总量,除以13亿都会变得很小”据国家统计局的公布,2004年我国淡水资源总量为26520亿立方米,居世界第四位,但人均只有 立方米,是全球人均水资源最贫乏的十三个国家之一。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC∽△DEF , 且△ABC的三边长分别为4,5,6,△DEF的一边长为2,则△DEF的周长为( )
A. 7.5 B. 6 C. 5或6 D. 5或6或7.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣a)(x﹣b)﹣2,(a<b)的图象与x轴交点的横坐标为m,n,且m<n,则a,b,m,n的大小关系是( )
A. m<a<b<n B. a<m<b<n C. a<m<n<b D. m<a<n<b
查看答案和解析>>
科目:初中数学 来源: 题型:
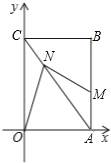
【题目】已知:矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正半轴上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点到达终点时,另一点即停止运动.设运动的时间为t秒.
(1)当点N运动1秒时,求点N的坐标;(提示:过N作x轴y轴垂线,垂足分别为D,ECN:CA=CE:CO=NE:OA)
(2)试求出多边形OAMN的面积S与t的函数关系式;
(3)t为何值时,以△OAN的一边所在直线为对称轴翻折△OAN,翻折前后的两个三角形所组成的四边形为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌服装原价800元,连续两次降价x%后售价为512元,下面所列方程中正确的是( )
A. 512(1+x%)2=800 B. 800(1﹣2x%)=512 C. 800(1﹣x%)2=512 D. 800﹣2x%=512
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com