
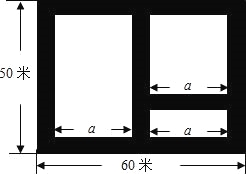
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
(1)设通道的宽度为x米,则a= (用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】根据图1,图2所提供的信息,解答下列问题:
(1)2007年海南省城镇居民人均可支配收入为 元,比2006年增长 %;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年 (填“增加”或“减少”).

查看答案和解析>>
科目:初中数学 来源: 题型:
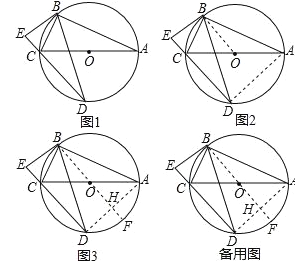
【题目】问题呈现:
如图1,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BE⊥DC交DC的延长线于点E.求证:BE是⊙O的切线.
问题分析:
连接OB,要证明BE是⊙O的切线,只要证明OB ____ BE,由题意知∠E=90°,故只需证明OB ___ DE.
解法探究:
(1)小明对这个问题进行了如下探索,请补全他的证明思路:
如图2,连接AD,由∠ECB是圆内接四边形ABCD的一个外角,可证∠ECB=∠BAD,因为OB=OC,所以 __ ,因为BD=BA,所以 ______ ,利用同弧所对的圆周角相等和等量代换,得到 ____ ,所以DE∥OB,从而证明出BE是⊙O的切线.
(2)如图3,连接AD,作直径BF交AD于点H,小丽发现BF⊥AD,请说明理由.
(3)利用小丽的发现,请证明BE是⊙O的切线.(要求给出两种不同的证明方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
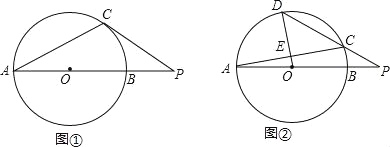
【题目】在⊙O中,AB为直径,C为⊙O上一点.
(Ⅰ)如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;
(Ⅱ)如图2,D为![]() 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线. 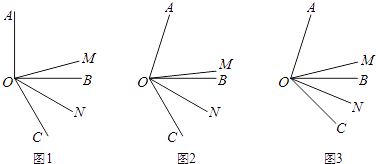
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON=(直接写出结果).
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON=(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
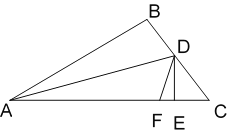
【题目】已知,如图,在△ABC中,AD平分∠BAC,DE、DF分别是△ADC的高和角平分线(∠C >∠DAC).
(1)若∠B=80°,∠C=40°,求∠DAE的度数;
(2)试猜想∠EDF、∠C与∠DAC有何种关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有除颜色外其余都相同的红、黄、蓝球共200个,墨墨通过多次摸球试验后发现,其中摸到红色球和蓝色球的频率稳定在25%和55%,则口袋中可能有黄球个.
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2平移得到抛物线y=x2+5,下列叙述正确的是( )
A.向上平移5个单位
B.向下平移5个单位
C.向左平移5个单位
D.向右平移5个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2﹣3B.y=﹣(x+1)2﹣3
C.y=﹣(x﹣1)2+3D.y=﹣(x+1)2+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com