
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= ![]() .
.
其中正确的结论有( )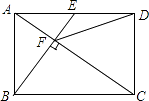
A.4个
B.3个
C.2个
D.1个
【答案】B
【解析】解:过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴ ![]() ,
,
∵AE= ![]() AD=
AD= ![]() BC,
BC,
∴ ![]() ,
,
∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE= ![]() BC,
BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,故③正确;
设AD=a,AB=b由△BAE∽△ADC,有 ![]() .
.
∵tan∠CAD= ![]() =
= ![]() ,
,
故④错误,
故选B.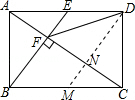
①四边形ABCD是矩形,BE⊥AC,则∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;②由AE= ![]() AD=
AD= ![]() BC,又AD∥BC,所以
BC,又AD∥BC,所以 ![]() ,故②正确;③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=
,故②正确;③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE= ![]() BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;④CD与AD的大小不知道,于是tan∠CAD的值无法判断,故④错误.
BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;④CD与AD的大小不知道,于是tan∠CAD的值无法判断,故④错误.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)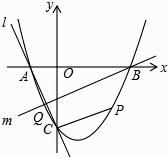
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期我们学习了“有理数乘方”运算,知道乘方的结果叫做“幂”,下面介绍一种有关“幂”的新运算.
定义:am 与 an(a≠0,m、n 都是正整数)叫做同底数幂,同底数幂除法记作 am÷an .
运算法则如下:am÷an=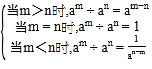
根据“同底数幂除法”的运算法则,回答下列问题:
(1)填空:![]() = ,43÷45= .
= ,43÷45= .
(2)如果 3x-1÷33x-4=![]() ,求出 x 的值.
,求出 x 的值.
(3)如果(x﹣1)2x+2÷(x﹣1)x+6=1,请直接写出 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
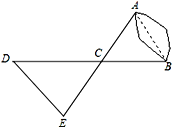
【题目】如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,小川从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.
(1)你能说明小川这样做的根据吗?
(2)如果小川恰好未带测量工具,但是知道A和假山D、雕塑C分别相距200米、120米,你能帮助他确定AB的长度范围吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
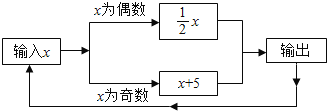
【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2017次输出的结果是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用白铁皮做罐头盒,每张铁皮可做盒身25个,或做盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?
①设用x张制盒身,可得方程2×25x=40(36﹣x);
②设用x张制盒身,可得方程25x=2×40(36﹣x);
③设用x张制盒身,y张制盒底,可得方程组![]() ;
;
④设用x张制盒身,y张制盒底,可得方程组![]() ;其中正确的是( )
;其中正确的是( )
A. ①④ B. ②③ C. ②④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块矩形场地,场地的长是宽的2倍.计划在矩形场地上修建宽都为2米的两条互相垂直的小路,如图,余下的四块小矩形场地建成草坪.四块小矩形草坪的面积之和为364平方米,求这个矩形场地的长和宽各是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com