
【题目】如图,△ABC中,∠BAC=110°,DE,FG分别为AB,AC的垂直平分线,E,G分别为垂足. 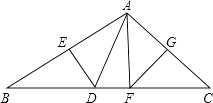
(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
【答案】
(1)解:设∠B=x,∠C=y.
∵∠BAC+∠B+∠C=180°,
∴110°+∠B+∠C=180°,
∴x+y=70°.
∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴∠EAD=∠B,∠FAC=∠C.
∴∠DAF=∠BAC﹣(x+y)=110°﹣70°=40°
(2)解:∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴△DAF的周长为:AD+DF+AF=BD+DF+FC=BC=10(cm).
【解析】(1)根据三角形内角和定理可求∠B+∠C;根据垂直平分线性质,DA=BD,FA=FC,则∠EAD=∠B,∠FAC=∠C,得出∠DAF=∠BAC﹣∠EAD﹣∠FAC=110°﹣(∠B+∠C)求出即可.(2)由(1)中得出,AD=BD,AF=FC,即可得出△DAF的周长为BD+FC+DF=BC,即可得出答案.


科目:初中数学 来源: 题型:
【题目】解答
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.
证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由. 
(3)拓展与应用:如图(3),D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?(只填写结果)
一个暖瓶 元;一个水杯 元.
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送二个水杯,单独买水杯不优惠.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
(3)若必须买5个暖瓶,则当买多少个水杯时到两家商城一样合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD.
∠BAD.
求证:EF=BE+FD;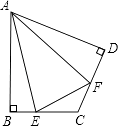
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立? 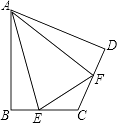
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明. 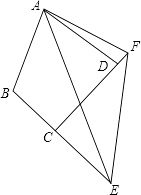
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角?(填“是”或“不是”).
(2)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com