
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
【答案】
(1)北偏东70°
(2)解:∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°-110°=70°
(3)解:∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°
【解析】解:(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,∴∠NOB=40°,∠NOA=15°,∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°.
故答案为北偏东70°;(1)根据题意可知∠NOB=40°,∠NOA=15°,先求出∠AOB的度数,再根据∠AOB=∠AOC,得出∠AOC的度数,然后根据∠NOC=∠NOA+∠AOC,求出∠NOC的度数,就可得出OC的方向.
(2)先根据∠AOC=∠AOB,求出∠BOC的度数,再根据∠COD=180°-∠BOC的度数即可。
(3)根据∠COD=70°,OE平分∠COD,求出∠COE的度数,再根据∠AOE=∠COE+∠AOC,计算即可得出答案。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在课间活动中,小英、小丽和小敏在操场上画出A,B两个区域,一起玩投包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每人各投沙包四次时,其落点和四次总分如图所示.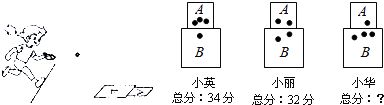
(1)沙包落在A区域和B区域所得分值分别是多少?
(2)求出小敏的四次总分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
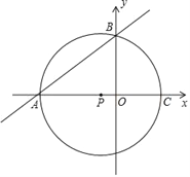
【题目】如图,点A的坐标为(﹣8,0),点P的坐标为(-![]() ,0),直线y=
,0),直线y=![]() x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了山更绿、水更清,某区大力实施生态修复工程,发展林业产业,确保到2021年实现全区森林覆盖率达到72.6%的目标.已知该区2019年全区森林覆盖率为60%,设从2019年起该区森林覆盖率年平均增长率为x,则x=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1 , B1 , C1 , 使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 , 记其面积为S1;第二次操作,分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使得A2B1=2A1B1 , B2C1=2B1C1 , C2A1=2C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , 记其面积为S2 , 则S2=。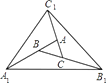
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2017排列成如下图所示的一个数表: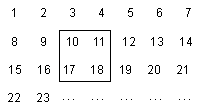
(1)用一正方形在表中随意框住4个数,把其中最小的数记为 ![]() ,另三个数用含
,另三个数用含 ![]() 的式子表示出来,从大到小依次是 , , ;
的式子表示出来,从大到小依次是 , , ;
(2)当被框住的4个数之和等于416时, ![]() 的值是多少?
的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时 ![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com