
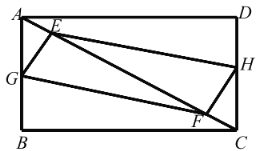
【题目】在矩形 ABCD 中,AB=3,BC=4,E、F 是对角线 AC 上的两个动点,分 别从 A、C 同时出发相向而行,速度均为每秒 1 个单位长度,运动时间为 t 秒,其中 0 t 5 .
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 是平行四边形(E、F 相遇时除外);
(2)在(1)条件下,若四边形 EGFH 为矩形,求 t 的值;
(3)若 G,H 分别是折线 A-B-C,C-D-A 上的动点,与 E,F 相同的速度同时出发,若 四边形 EGFH 为菱形,求 t 的值.
【答案】(1)见解析;(2)0.5或4.5;(3)![]()
【解析】
(1)根据勾股定理求出AC,证明△AFG≌△CEH,根据全等三角形的性质得到GF=HE,同理得到GE=HF,根据平行四边形的判定定理证明;
(2)分AE=CF、AE=CF两种情况,根据矩形的性质计算即可;
(3)连接AG、CH,判定四边形AGCH是菱形,得到AG=CG,根据勾股定理求出BG,得到AB+BG的长,根据题意解答.
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=![]() ,∠GAF=∠HCE,
,∠GAF=∠HCE,
∵G,H分别是AB,DC中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG和△CEH中,
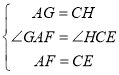 ,
,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形;
(2)解:由(1)得:BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=4,当EF=GH=4时,平行四边形EGFH是矩形,
分两种情况:①AE=CF=t,EF=5-2t=4,
解得:t=0.5;
②AE=CF=t,EF=5-2(5-t)=4,
解得:t=4.5;
综上所述:当t为0.5s或4.5s时,四边形EGFH为矩形;
(3)解:连接AG、CH,如图所示:
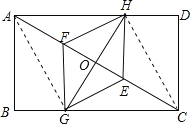
∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH,OE=OF,
∴OA=OC,AG=AH,
∴四边形AGCH是菱形,
∴AG=CG,
设AG=CG=x,则BG=4-x,
由勾股定理得:AB2+BG2=AG2,
即32+(4-x)2=x2,
解得,x=![]() ,
,
∴BG=![]() =
=![]() ,
,
∴AB+BG=3+![]() =
=![]() ,
,
∴t为![]() 时,四边形EGFH为菱形.
时,四边形EGFH为菱形.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(0,10),点B(m,10)在第一象限,连接AB、OB.
(1)如图1,若OB=12,求m的值.

(2)如图2,当m=10时,过B作BC⊥x轴于C,E为AB边上一点,AE=![]() ,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.
,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.

(3)如图3,将△AOB沿直线OB翻折得到△GOB(点A的对应点为点G),若点G到x轴的距离不大于8,直接写出m的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,连接BD,AB=2AD,点E在AB边上,连接ED.
(1)若∠ADE=30°,DE=6,求△BDE的面积;
(2)延长CB至点F使得BF=2AD,连接FE并延长交AD于点M,过点A作AN⊥EM于点N,连接BN,求证:FN=AN+![]() BN.
BN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方形分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
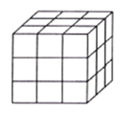
(1)只有一面涂有颜色的概率;
(2)至少有两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;

图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.

图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABC中∠A=60°,AB=2cm,AC=6cm,点P、Q分别是边AB、AC上的动点,点P从顶点A沿AB以1cm/s的速度向点B运动,同时点Q从顶点C沿CA以3cm/s的速度向点A运动,当点P到达点B时点P、Q都停止运动.设运动的时间为t秒.

(1)当t为何值时AP=AQ;
(2)是否存在某一时刻使得△APQ是直角三角形,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com