
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
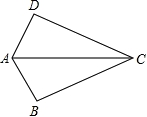
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
C【考点】全等三角形的判定.
【分析】本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.
【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;
故选:C.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:A AA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
AA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:
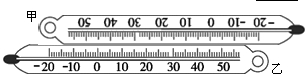
甲、乙两支同样的温度计如图所示放置,如果向左移动甲温度计,使其度数5正对着乙温度计的度数﹣18,那么此时甲温度计的度数﹣7正对着乙温度计的度数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,如图下列条件中,不能证明△ABD≌△ACD的是( )
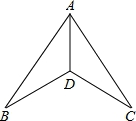
A.BD=DC,AB=AC B.∠ADB=∠ADC,∠BAD=∠CAD
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
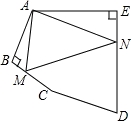
如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com