
如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为__________.
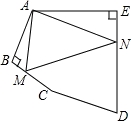
88°.
【考点】轴对称-最短路线问题.
【分析】根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=44°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
【解答】解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠BAE=136°,
∴∠HAA′=44°,
∴∠A′+∠A″=∠HAA′=44°,
∵∠A′=∠MAA′,∠NAE=∠A″,
且∠A′+∠MAA′=∠AMN,∠NAE+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAE+∠A″=2(∠A′+∠A″)=2×44°=88°,
故答案为:88°.
【点评】此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
在下列数:3.14,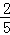 ,3.3333…,0,0.4
,3.3333…,0,0.4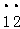 ,﹣π,0.10110111011110…中,无理数的个数有( )
,﹣π,0.10110111011110…中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是__________.(不再添加辅助线和字母)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
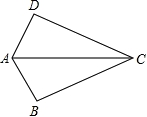
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中,正确的是( )
A.正数和负数统称为有理数
B.互为相反数的两个数之和为零
C.如果两个数的绝对值相等,那么这两个数一定相等
D.0是最小的有理数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com