
如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是__________.(不再添加辅助线和字母)

答案不唯一,如AB=AC或∠B=∠C
或∠BED=∠CFD或∠AED=∠AFD.(不再添加辅助线和字母)
【考点】全等三角形的判定与性质.
【专题】开放型.
【分析】答案不唯一根据AB=AC,推出∠B=∠C,根据ASA证出△BED和△CFD全等即可;添加∠BED=∠CDF,根据AAS即可推出△BED和△CFD全等;根据∠AED=∠AFD推出∠B=∠C,根据ASA证△BED≌△CFD即可.
【解答】解:答案不唯一,如AB=AC或∠B=∠C或∠BED=∠CFD,或∠AED=∠AFD等;
理由是:①∵AB=AC,
∴∠B=∠C,
根据ASA证出△BED≌△CFD,即可得出DE=DF;
②由∠B=∠C,∠BDE=∠CDF,BD=DC,根据ASA证出△BED≌△CFD,即可得出DE=DF;
③由∠BED=∠CFD,∠BDE=∠CDF,BD=DC,根据AAS证出△BED≌△CFD,即可得出DE=DF;
④∵∠AED=∠AFD,∠AED=∠B+∠BDE,∠AFD=∠C+∠CDF,
又∵∠BDE=∠CDF,
∴∠B=∠C,
即由∠B=∠C,∠BDE=∠CDF,BD=DC,根据ASA证出△BED≌△CFD,即可得出DE=DF;
故答案为:答案不唯一,如AB=AC或∠B=∠C或∠BED=∠CFD或∠AED=∠AFD.
【点评】本题考查了全等三角形的判定,题目具有一定的代表性,是一道比较好的题目.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
有理数a、b、c在数轴上的位置如图:
观察下列有规律的数: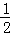 ,
,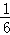 ,
,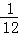 ,
,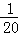 ,
,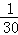 ,
,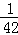 …根据规律可知
…根据规律可知
(1)第7个数__________,第n个数是__________(n是正整数)
(2)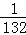 是第__________个数
是第__________个数
(3)计算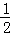 +
+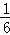 +
+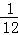 +
+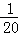 +
+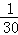 +
+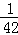 +…+
+…+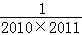 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,如图下列条件中,不能证明△ABD≌△ACD的是( )
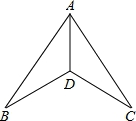
A.BD=DC,AB=AC B.∠ADB=∠ADC,∠BAD=∠CAD
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( )
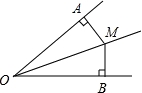
A.50° B.40° C.30° D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为__________.
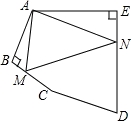
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)观察一列数a1=3,a2=9,a3=27,a4=81,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是__________;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么 a6=__________,an=__________;(可用幂的形式表示)
(2)如果想要求1+2+22+23+…+210的值,可令S10=1+2+22+23+…+210①将①式两边同乘以2,得__________②,由②减去①式,得S10=__________.
(3)若(1)中数列共有20项,设S20=3+9+27+81+…+a20,请利用上述规律和方法计算S20(列式计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com