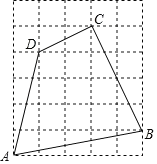
【题目】如图，每个小正方形的边长为1．
（1）直接写出四边形ABCD的面积和周长；
（2）求证：∠BCD=90°．
【答案】（1）四边形ABCD的面积为14.5，四边形ABCD的周长是
3
；（2）证明见解析．
【解析】
（1）用四边形ABCD所在长方形的面积减去4个小三角形的面积，列出算式计算即可求得四边形ABCD的面积；利用勾股定理分别求出AB、BC、CD、AD，即可求得四边形ABCD的周长；
（2）求出BD2，利用勾股定理的逆定理即可证明；
（1）四边形ABCD的面积=5×5﹣3×1÷2﹣4×2÷2﹣5×1÷2﹣5×1÷2=14.5；
由勾股定理得AB
，BC
2
，CD
，AD
，
故四边形ABCD的周长是2
3；
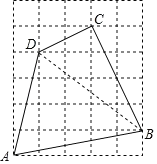
（2）连接BD．
∵BD2
，BC2+CD2=20+5=25，
∴BC2+CD2=BD2，
∴△BCD是直角三角形，且∠BCD=90°．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析。下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下：
(说明：成绩80分及以上为优秀,7079分为良好,6069分为合格,60分以下为不合格)
b.甲校成绩在70x<80这一组的是：70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下：
根据以上信息，回答下列问题：
(1)写出表中n的值；
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是___校的学生(填“甲”或“乙”)，理由是___；
(3)假设乙校800名学生都参加此次测试，估计成绩优秀的学生人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店出售一种商品，其原价为
元，现有两种调价方案：一种是先提价
，在此基础上又降价；另一种是先降价， 在此基础上又提价.
1)用这两种方案调价的结果是否一样?
2)两种调价方案改为：一种是提价
；另一种是先提价
，在此基础上又提价
，这两种调价方案结果是否一样?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC在平面直角坐标系中的位置如图所示.
（1）作出△ABC关于
轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标；
（2）将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；
（3）观察△A1B1C和△A2B2C2，它们是否关于某直线对称？若是，请用实线条画出对称轴。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将二次函数y=x2-m（其中m＞0）的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，形成新的图象记为y1，另有一次函数y=x+b的图象记为y2，则以下说法：
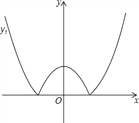
①当m=1，且y1与y2恰好有三个交点时b有唯一值为1；
②当b=2，且y1与y2恰有两个交点时，m＞4或0＜m＜
；
③当m=-b时，y1与y2一定有交点；
④当m=b时，y1与y2至少有2个交点，且其中一个为（0，m）．
其中正确说法的序号为 ______ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，函数y=kx+b（k≠0）的图象经过点B（2，0），与函数y=2x的图象交于点A，则不等式0＜kx+b＜2x的解集为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．
（1）求证：DE是⊙O的切线；
（2）若AE=6，∠D=30°，求图中阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系的图象如图所示．
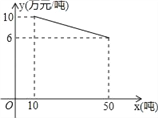
（1）求y关于x的函数解析式，并写出x的取值范围；
（2）当生产这种产品每吨的成本为7万元时，求该产品的生产数量．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，抛物线
（ a≠0）经过原点，顶点为A（h，k）（h≠0）．
（1）当h＝1，k＝2时，求抛物线的解析式；
（2）若抛物线
（t≠0）也经过A点，求a与t之间的关系式；
（3）当点A在抛物线
上，且－2≤h＜1时，求a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com